第2节 一文搞定还原二叉树问题

二叉树是一个重要的数据结构，学习好二叉树很重要，本文将借助leetcode三道练习题，从前序+后序、前序+中序以及中序+后序三种遍历组合方式来还原二叉树。

一、二叉树的遍历

首先我们一起来温习下二叉树的三种遍历方式：前序遍历、中序遍历、后续遍历。如果读者不太了解这三种遍历方式，建议找点博客看看二叉树的三种遍历，本文主要是借助二叉树的遍历结果来还原二叉树，所以本文默认读者是了解二叉树的遍历的。

首先我们一起看下二叉树的三种遍历方式，如下图所示一棵二叉树：

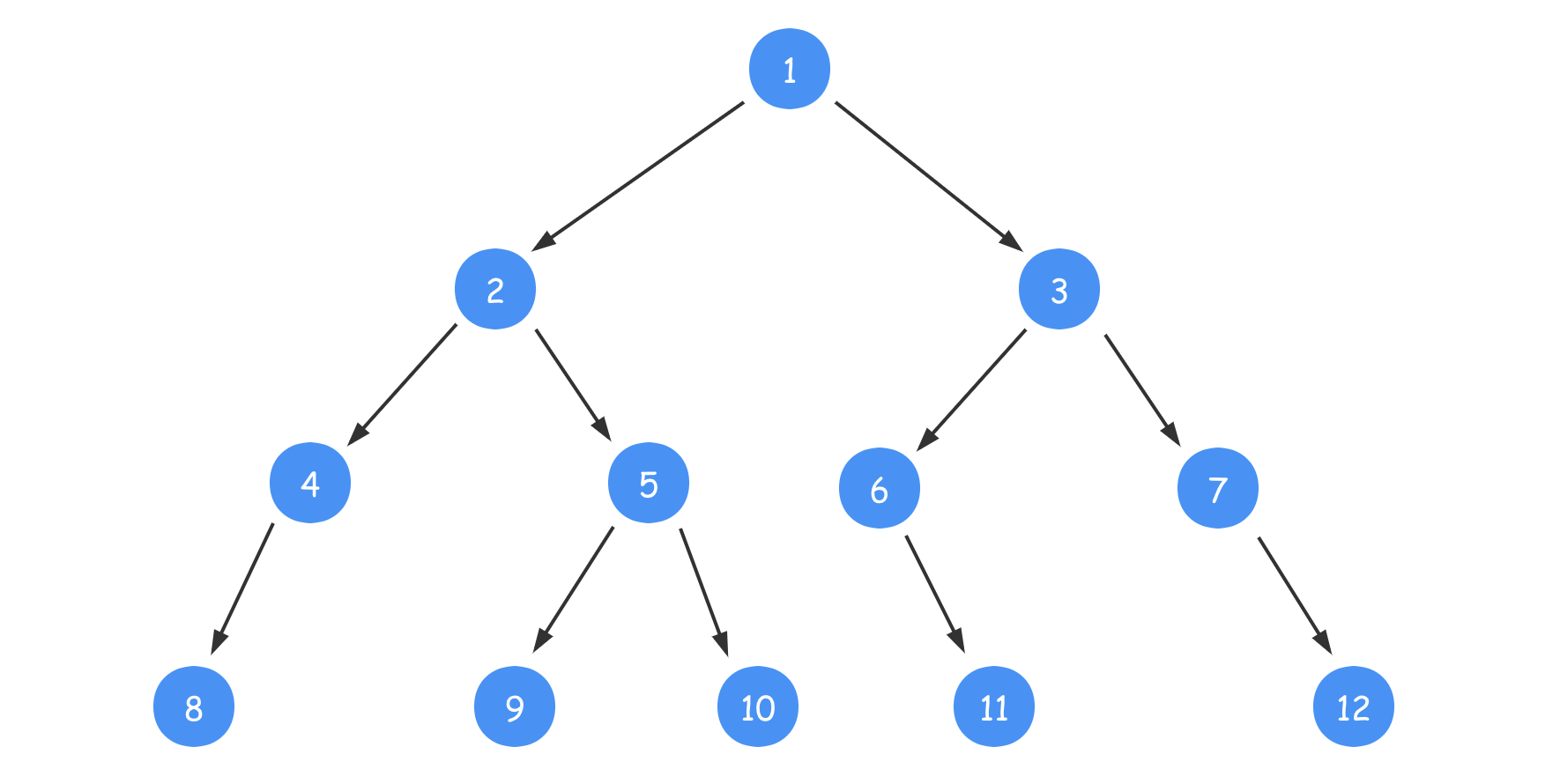
三种遍历结果如下所示：

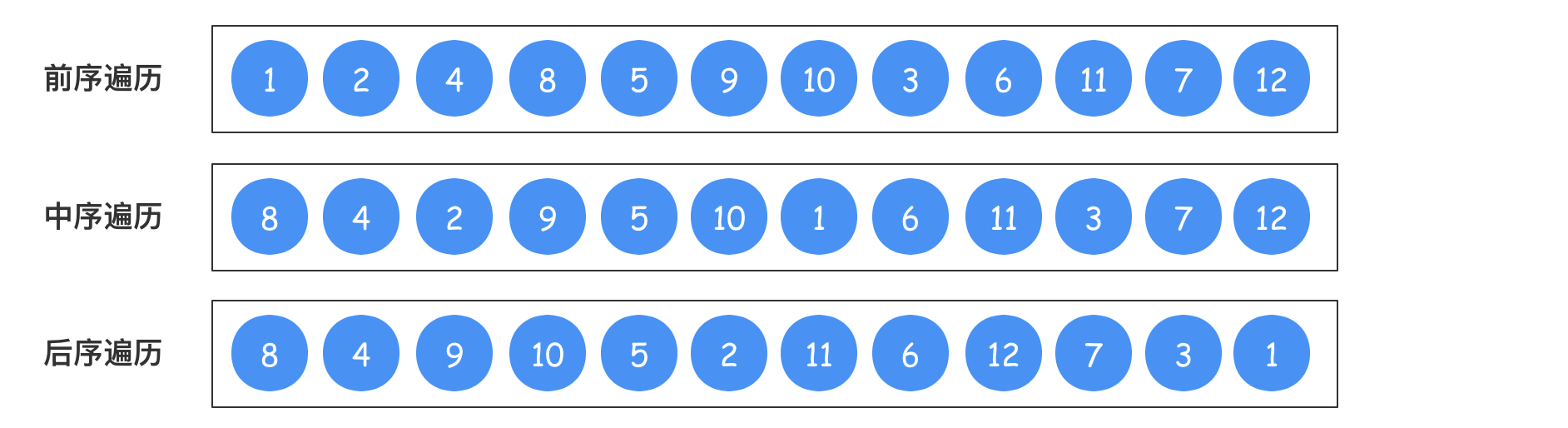
三种遍历方式的区别是：根何时遍历。

• 前序遍历是先遍历根，再分别遍历左右子树，左右子树中也是先遍历子树的根，简称根左右；
• 中序遍历是先遍历左子树，再遍历根，最后遍历右子树，左右子树中也是如此，简称左根右；
• 后续遍历是先遍历左子树，再遍历右子树，最后遍历根，左右子树中也是如此，简称左右根。

二、根据前序和中序遍历构造二叉树

本小节，我们以前序遍历的结果和中序遍历的结果来还原二叉树，为了文章的完整性，就采用上面的二叉树的遍历结果来进行二叉树的还原，弄懂了这小节，那么就可以将leetcode第105题 从前序与中序遍历序列构造二叉树 做出来，讨论的问题是一样的。

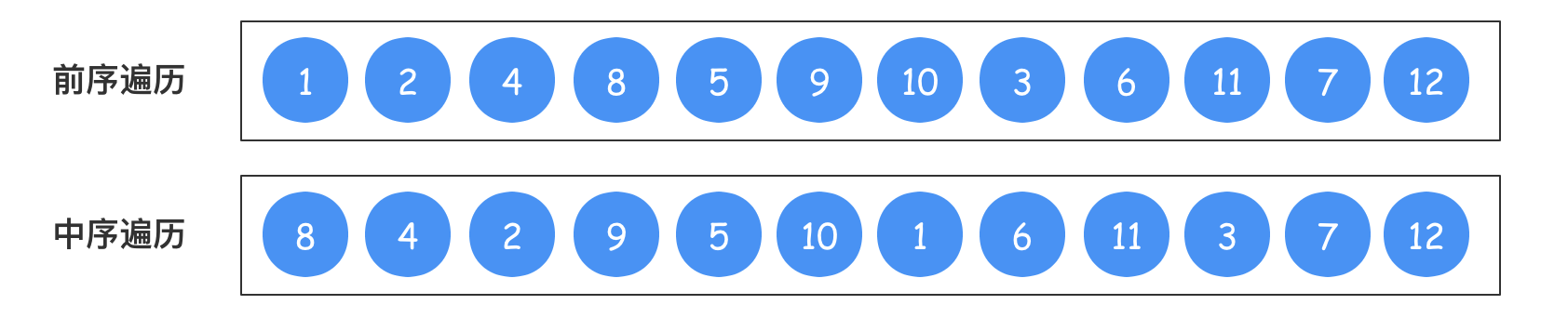
根据上面的前序遍历和中序遍历，该如何正确还原成一棵二叉树呢？其实需要用到前序遍历和中序遍历的两个基本特性：

• 在前序遍历结果中，第一个位置的元素是二叉树的根节点；
• 在中序遍历结果中，根节点的左边为左子树，根节点的右边为右子树。

那么根据这两个特性，我们很容易确定二叉树的左子树和右子树，以及左右子树节点的个数等基本信息。

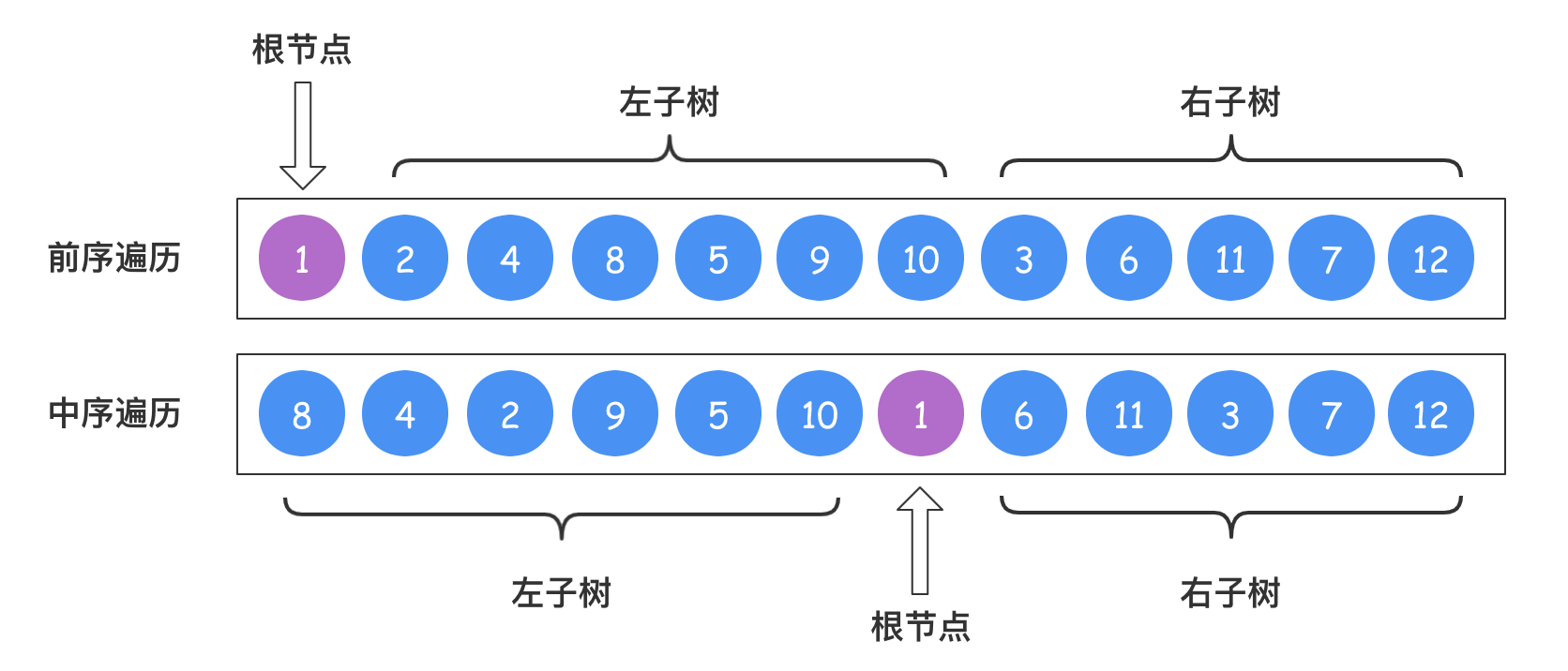
上图中，在前序遍历中将根节点确定下来之后，在中序遍历中就可以将根节点的左右子树都确定出来。因为前序遍历属于深度优先遍历，也就是“一挖到底”，所以从上图中可以知道左子树的根节点是2，右子树的根节点是3，那么在中序遍历中可以进一步找到左右子树的左右子树，那么这个问题就可以进一步缩小，且符合递归的规律，所以完全可以使用递归来解决这个问题。

为了还原二叉树，我们一起来定义几个变量，方便后续分析树的还原过程：

• 定义一个Map，用来记录中序遍历结果中个元素与下标索引的对应关系，这样我们可以快速地获取到某个元素在中序遍历结果中的具体位置，比如根节点，我们就可以用根节点将中序遍历结果一分为二，将左右子树都分隔出来，后续左右子树的左右子树也能快速的分隔出来；
• 定义一个int类型的ri，表示rootIndex，根节点的索引；
• 定义一个int类型的leftChildTreeNodeNum，表示左子树的节点个数；
• 在前序遍历结果中定义两个位置变量[ps, pe]，ps表示前序遍历结果序列的起始位置，pe表示前序遍历结果序列的结束位置；
• 在中序遍历结果中定义两个位置变量[is, ie]，is表示中序遍历结果序列的起始位置，ie表示中序遍历结果序列的结束位置。

有了上述变量，我们来分析下二叉树的还原过程中的边界情况：

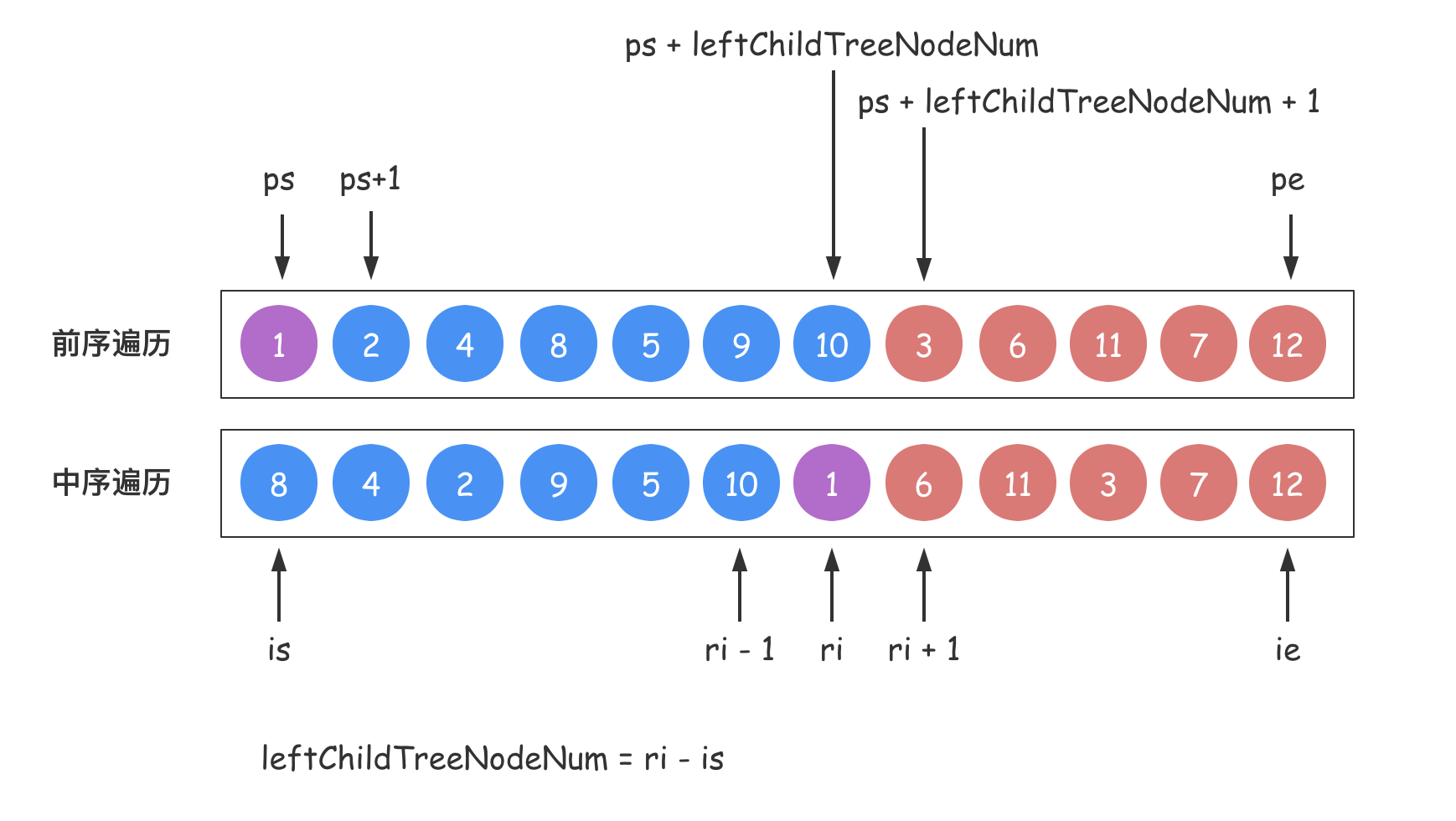从上图中，我们可以分析成文字如下所示：

• 在找根节点的时候，都是以这两个整体序列为基础的，所以前序遍历序列的起止位置是[ps, pe]，即为[0, preorder.length - 1]，中序遍历序列的起止位置是[is, ie]，即为[0, inorder.length - 1]；
• 那么在处理左子树的时候，需要在这两个序列中将左子树的部分截取出来，所以在前序遍历序列中的起止位置是[ps + 1, ps + leftChildTreeNodeNum]，在中序遍历序列中的起止位置为：[is, ri - 1]；
• 那么在处理右子树的时候，也同样需要在这两个序列中将右子树的部分截取出来，所以在前序遍历序列中的起止位置是[ps + leftChildTreeNodeNum + 1, pe]，在中序遍历序列中的起止位置为：[ri + 1, ie]；

按照上面的分析结果，边界弄清楚了，那么代码写起来也就方便了，代码如下所示：

/**
 * 递归法
 *
 * @param preorder 前序遍历列表
 * @param inorder 中序遍历列表
 * @return 二叉树
 */
public TreeNode buildTree(int[] preorder, int[] inorder) {
    Map<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < inorder.length; i++) {
        map.put(inorder[i], i);
    }
    return buildTreeHelper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1, map);
}

private TreeNode buildTreeHelper(int[] preorder, int ps, int pe, int[] inorder, int is, int ie,
        Map<Integer, Integer> map) {
    // 递归终止条件
    if (pe < ps || ie < is) {
        return null;
    }

    // 递归本层次需要做的事情
    // 获取根节点
    TreeNode root = new TreeNode(preorder[ps]);
    // 获取根节点在中序遍历结果序列中的位置
    int ri = map.get(preorder[ps]);
    // 确定左子树的数量，从而可以从前序遍历中找到左子树和右子树
    int leftChildTreeNodeNum = ri - is;

    // 递归过程
    root.left = buildTreeHelper(preorder, ps + 1, ps + leftChildTreeNodeNum, inorder, is, ri - 1, map);
    root.right = buildTreeHelper(preorder, ps + leftChildTreeNodeNum + 1, pe, inorder, ri + 1, ie, map);
    return root;
}

代码看起来是不是很简单？其实这类题只要把规律找到了，边界弄清楚了，写出代码那就是顺理成章的事情了。我们趁热打铁，一起接着看看后面的两小节。

三、根据前序和后序遍历构造二叉树

本小节，我们以前序遍历的结果和后序遍历的结果来还原二叉树，为了文章的完整性，就采用上面的二叉树的遍历结果来进行二叉树的还原，弄懂了这小节，那么就可以将leetcode第889题 根据前序和后序遍历构造二叉树 做出来，讨论的问题是一样的。

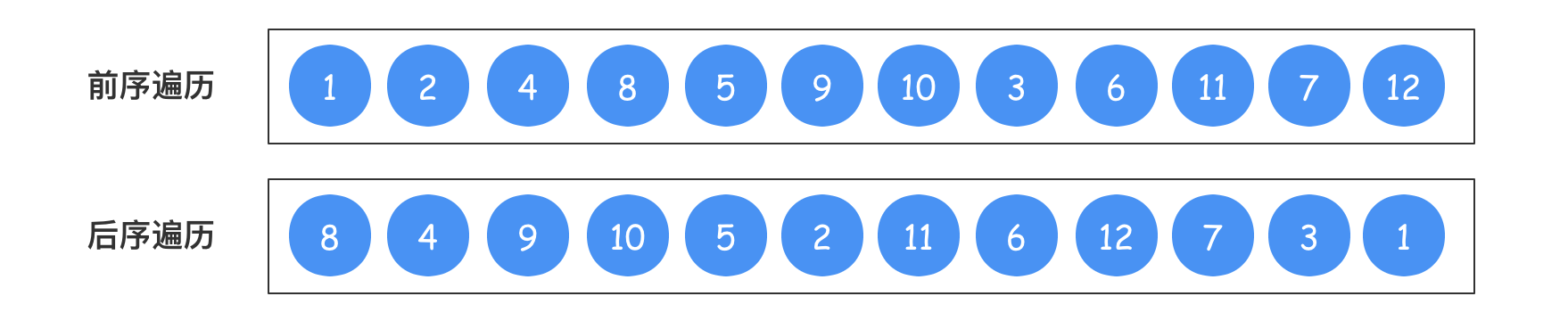
根据上面的前序遍历和后序遍历，该如何正确还原成一棵二叉树呢？其实需要用到前序遍历和后序遍历的两个基本特性：

• 在前序遍历结果中，第一个位置的元素是二叉树的根节点，如果有左子树，那么第二个位置的元素是左子树的子树根节点；
• 在后序遍历结果中，最后一个位置的元素是根节点，如果有右子树，那么倒数第二个位置的元素一定是右子树的子树根节点。

那么根据这两个特性，我们很容易确定二叉树的左子树和右子树，以及左右子树节点的个数等基本信息。

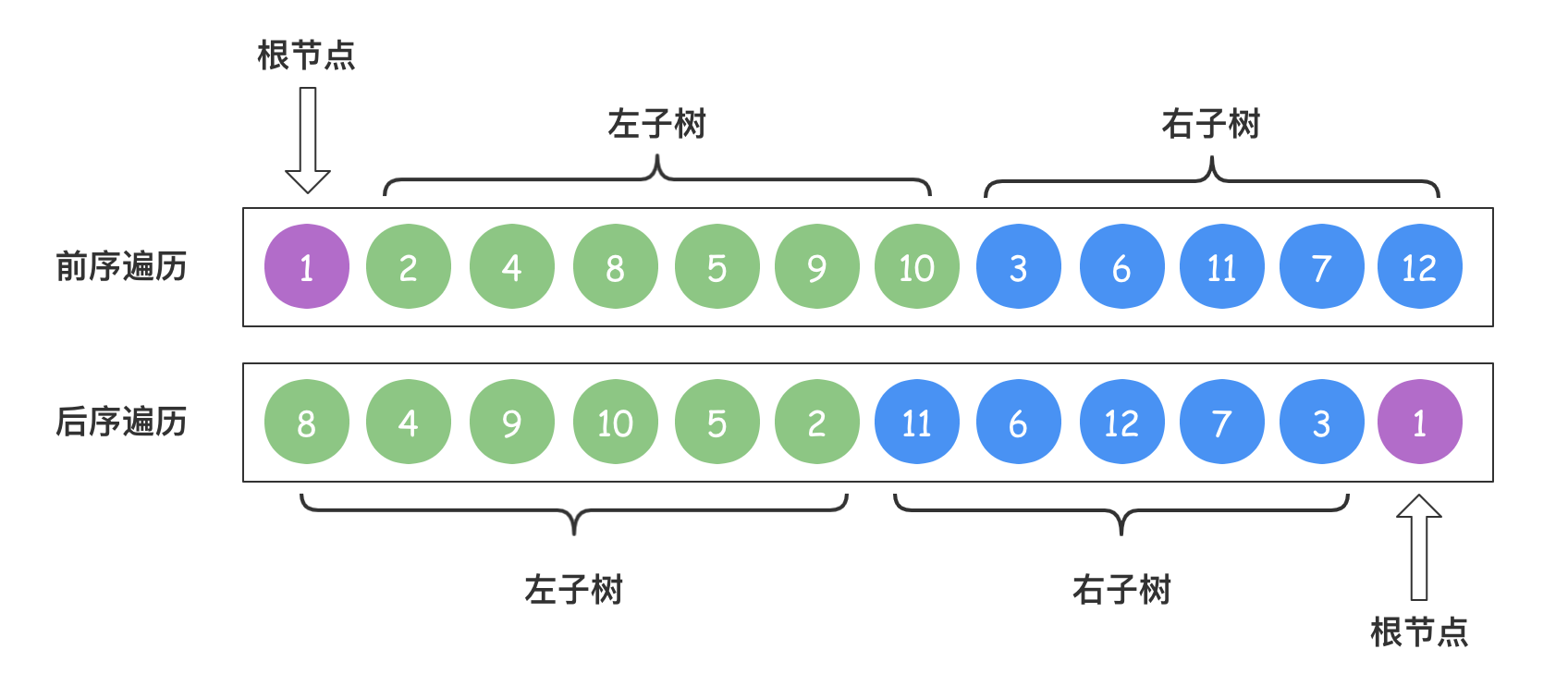
上图中，在前序遍历和后序遍历中将根节点确定下来之后，结合前序遍历和后序遍历的特点，就可以将根节点的左右子树都确定出来。因为前序遍历属于深度优先遍历，也就是“一挖到底”，所以从上图中可以知道左子树的根节点是2，右子树的根节点是3，那么在中前序遍历和后序遍历中可以进一步找到左右子树的左右子树，那么这个问题就可以进一步缩小，且符合递归的规律，所以完全可以使用递归来解决这个问题。

为了还原二叉树，我们一起来定义几个变量，方便后续分析树的还原过程：

• 定义一个Map，用来记录后序遍历结果中个元素与下标索引的对应关系，这样我们可以快速地获取到某个元素在后序遍历结果中的具体位置，比如左子树的子树根节点，我们就可以用它将后序遍历结果一分为二，将左右子树都分隔出来，后续左右子树的左右子树也能快速的分隔出来；
• 定义一个int类型的leftRootIndex，表示左子树子树根节点的索引；
• 定义一个int类型的leftChildTreeNodeNum，表示左子树的节点个数；
• 在前序遍历结果中定义两个位置变量[ps, pe]，ps表示前序遍历结果序列的起始位置，pe表示前序遍历结果序列的结束位置；
• 在后序遍历结果中定义两个位置变量[pos, poe]，pos表示后序遍历结果序列的起始位置，poe表示后序遍历结果序列的结束位置。

有了上述变量，我们来分析下二叉树的还原过程中的边界情况：

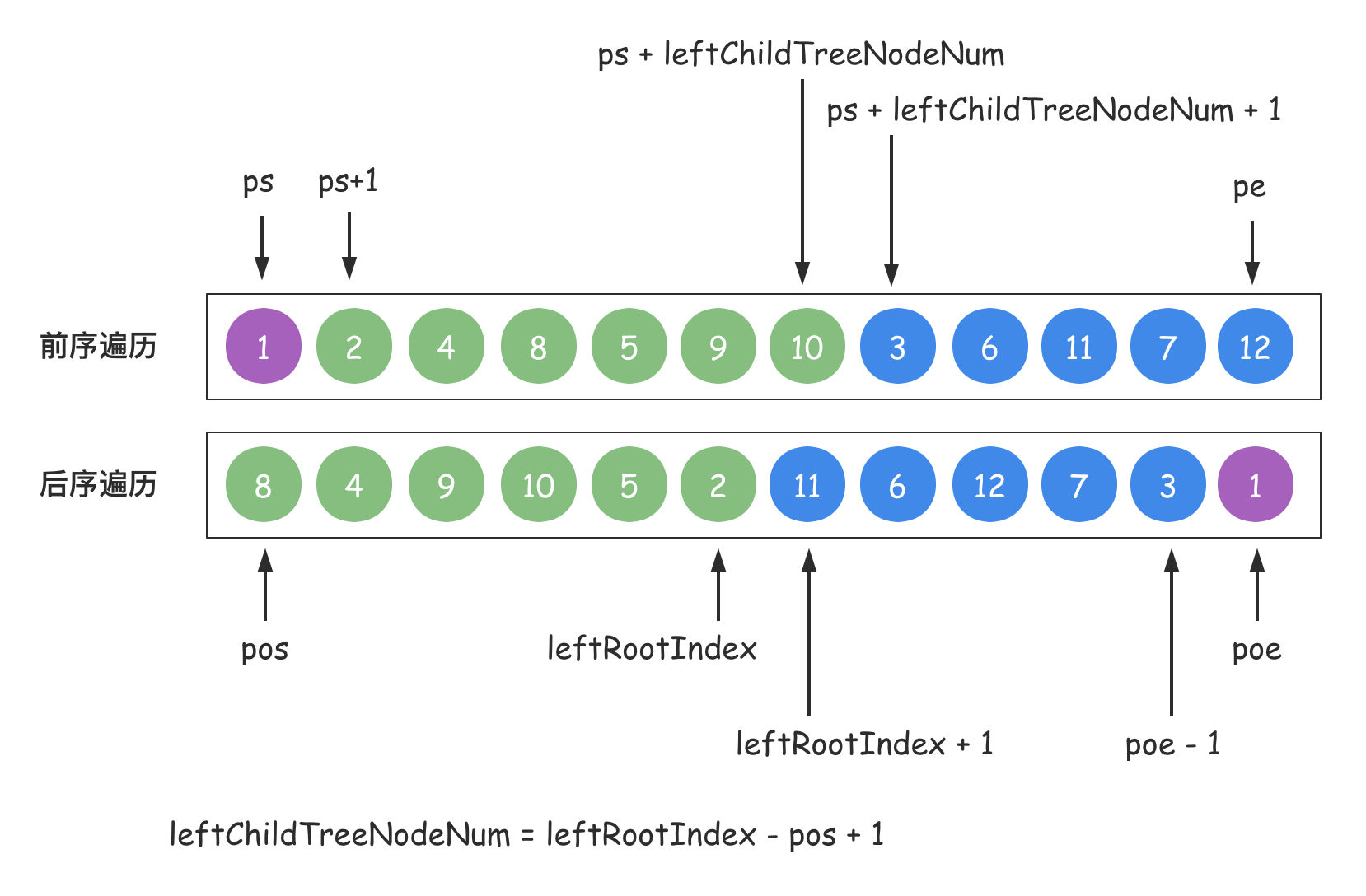从上图中，我们可以分析成文字如下所示：

• 在找根节点的时候，都是以这两个整体序列为基础的，所以前序遍历序列的起止位置是[ps, pe]，即为[0, pre.length - 1]，后序遍历序列的起止位置是[pos, poe]，即为[0, post.length - 1]；
• 那么在处理左子树的时候，需要在这两个序列中将左子树的部分截取出来，所以在前序遍历序列中的起止位置是[ps + 1, ps + leftChildTreeNodeNum]，在后序遍历序列中的起止位置为：[pos, leftRootIndex]；
• 那么在处理右子树的时候，也同样需要在这两个序列中将右子树的部分截取出来，所以在前序遍历序列中的起止位置是[ps + leftChildTreeNodeNum + 1, pe]，在后序遍历序列中的起止位置为：[leftRootIndex + 1, poe - 1]；

按照上面的分析结果，边界弄清楚了，那么代码写起来也就方便了，代码如下所示：

/**
 * 递归解法
 *
 * @param pre 前序遍历序列
 * @param post 后序遍历序列
 * @return 还原后的二叉树
 */
public TreeNode constructFromPrePost(int[] pre, int[] post) {
    Map<Integer, Integer> map = new HashMap<>((int) (post.length / 0.75) + 1);
    for (int i = 0; i < post.length; i++) {
        map.put(post[i], i);
    }
    return buildTreeHelper(pre, 0, pre.length - 1, post, 0, post.length - 1, map);
}

private TreeNode buildTreeHelper(int[] pre, int ps, int pe, int[] post, int pos, int poe,
        Map<Integer, Integer> map) {
    // 递归终止条件
    if (pe < ps || poe < pos) {
        return null;
    }

    // 递归本层次需要做的事情
    // 获取根节点
    TreeNode root = new TreeNode(pre[ps]);
    // 获取左子树的根节点在后序遍历序列中的索引
    // 注意这里有个隐含的边界条件需要判断，判断ps+1是否越界
    if (ps + 1 > pe) {
        return root;
    }
    int leftRootIndex = map.get(pre[ps + 1]);
    // 确定左子树的数量，从而可以从前序遍历中找到左子树和右子树
    int leftChildTreeNodeNum = leftRootIndex - pos + 1;

    // 递归过程
    root.left = buildTreeHelper(pre, ps + 1, ps + leftChildTreeNodeNum, post, pos, leftRootIndex, map);
    root.right =
            buildTreeHelper(pre, ps + leftChildTreeNodeNum + 1, pe, post, leftRootIndex + 1, poe - 1, map);
    return root;
}

其实这类题的解题思路都是一样的，把边界弄清楚了，用递归的方式很容易就可以解决问题。

四、根据中序和后序遍历构造二叉树

我们已经一起解决了根据前序和中序，前序和后序的遍历结果序列来还原二叉树，现在我们一起看下这个题型的最后一道题：根据中序和后序的遍历构造二叉树。通过前面两道题的训练，我相信读者都可以独立将这道题做出来，其实思想也是很简单，就是利用中序和后序遍历序列的特性，找到左右子树的边界，那么这道题就基本解决了。读者读到这里，可以暂停下，想想该如何解决这道题。

本小节讨论的问题和leetcode 106题一样：从中序与后序遍历序列构造二叉树 ，我们目前还是以前面的二叉树为例，这里列出中序遍历和后序遍历序列如下：

根据上面的中序序遍历和后序遍历，该如何正确还原成一棵二叉树呢？其实需要用到中序遍历和后序遍历的两个基本特性，我想，说到这， 读者肯定知道它们的特性了，因为前面两小节都已经阐述过了，没错，就是下面两个基本点：

• 在后序遍历结果中，最后一个位置的元素是二叉树的根节点；
• 在中序遍历结果中，根节点的左边为左子树，根节点的右边为右子树。

那么根据这两个特性，我们很容易确定二叉树的左子树和右子树，以及左右子树节点的个数等基本信息。

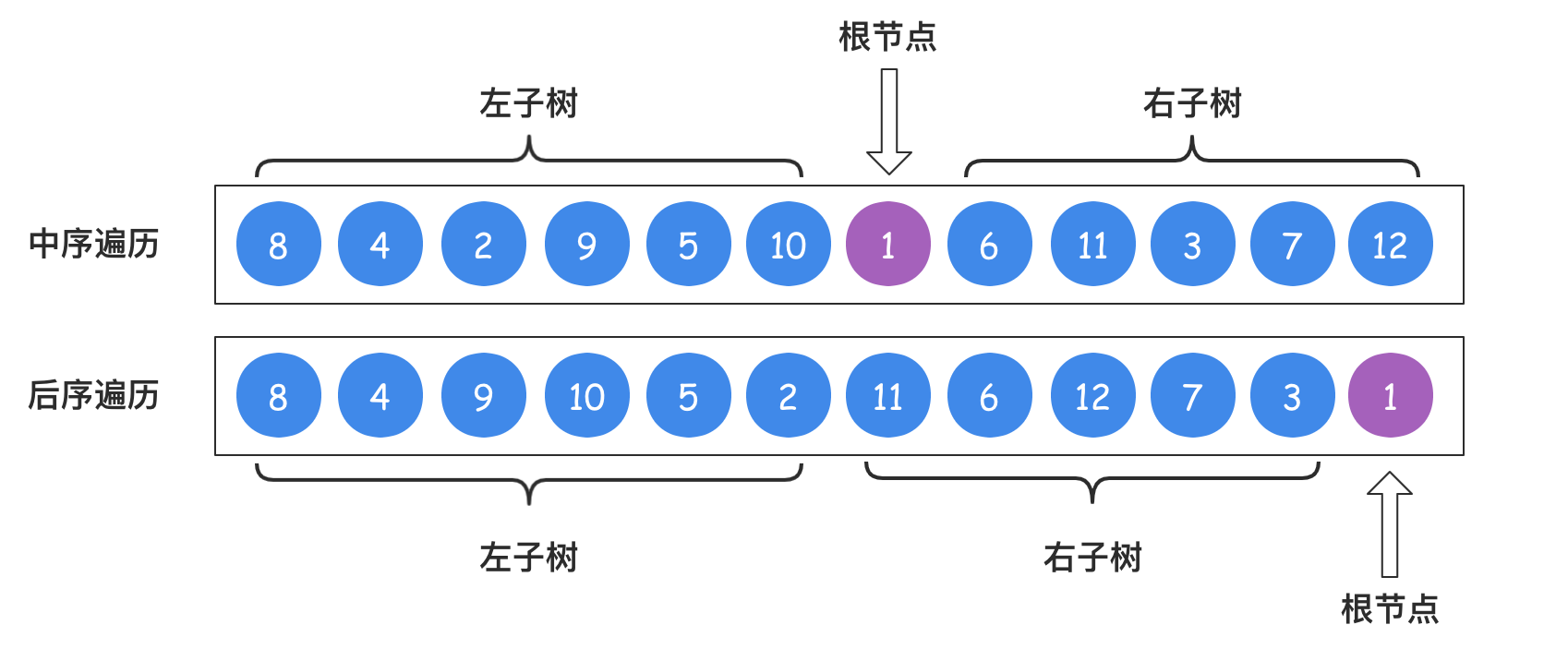我们从后序遍历中可以直接定位到整棵树的根节点，就是后序遍历序列中的最后一个位置的元素，在中序遍历中找到根节点的位置，以根节点为划分线，可以将中序遍历序列一分为二，左边是左子树，右边是右子树。

我们定义几个变量，如下所示：

• 定义一个Map，用来记录中序遍历结果中个元素与下标索引的对应关系，这样我们可以快速地获取到某个元素在中序遍历结果中的具体位置，比如根节点，我们就可以用根节点将中序遍历结果一分为二，将左右子树都分隔出来，后续左右子树的左右子树也能快速的分隔出来；

• 定义一个int类型的ri，表示rootIndex，根节点在中序遍历中的索引；

• 定义一个int类型的leftChildTreeNodeNum，表示左子树的节点个数；

• 在中序遍历结果中定义两个位置变量[is, ie]，is表示中序遍历结果序列的起始位置，ie表示中序遍历结果序列的结束位置；

• 在后序遍历结果中定义两个位置变量[pos, poe]，pos表示前序遍历结果序列的起始位置，poe表示前序遍历结果序列的结束位置。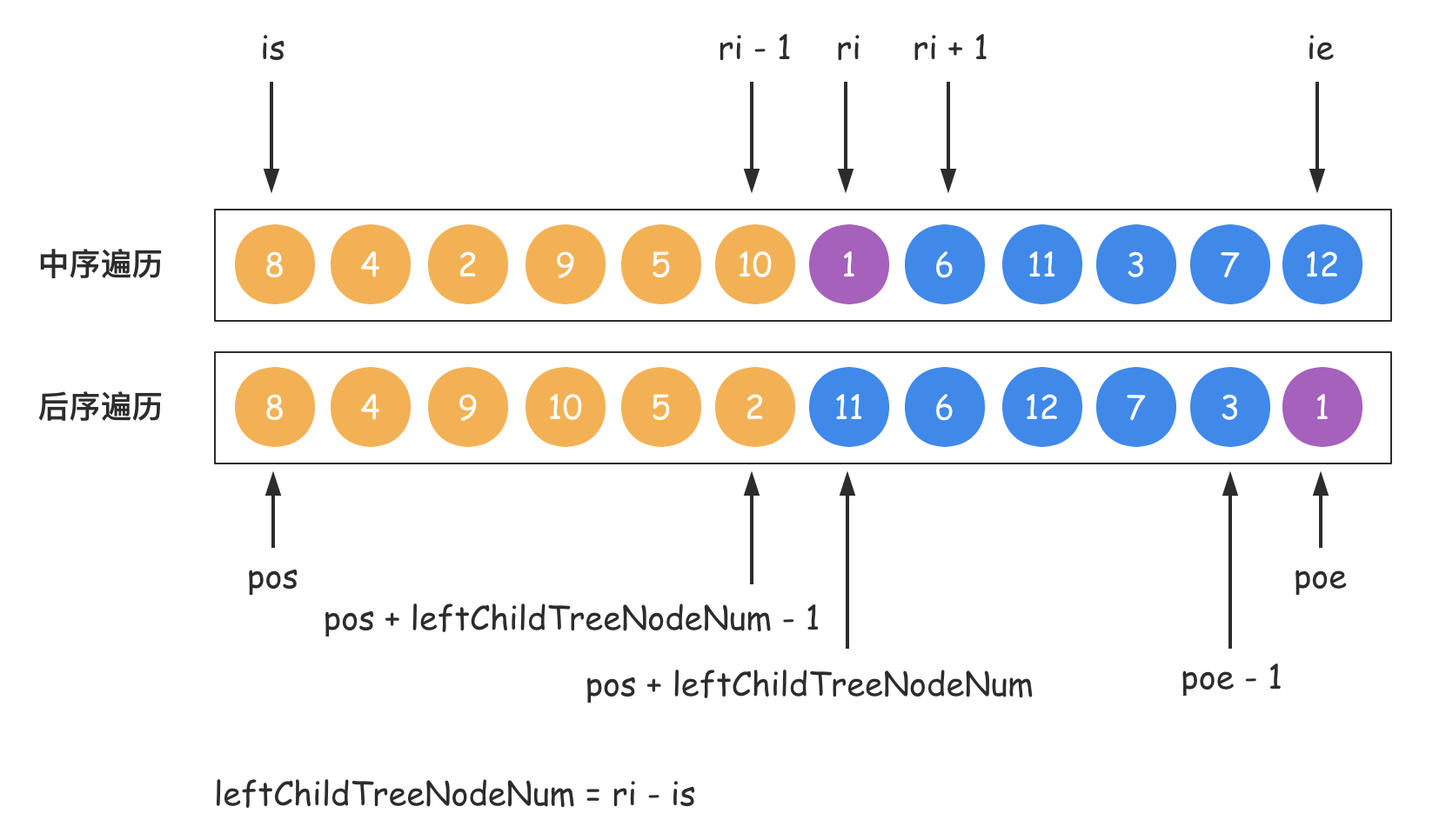

  

从上图中，我们可以分析成文字如下所示：

• 在找根节点的时候，都是以这两个整体序列为基础的，所以中序遍历序列的起止位置是[is, ie]，即为[0, inorder.length - 1]，后序遍历序列的起止位置是[pos, poe]，即为[0, postorder.length - 1]；
• 那么在处理左子树的时候，需要在这两个序列中将左子树的部分截取出来，所以在中序遍历序列中的起止位置是[is, ri - 1]，在后序遍历序列中的起止位置为：[pos, pos + leftChildTreeNodeNum - 1]；
• 那么在处理右子树的时候，也同样需要在这两个序列中将右子树的部分截取出来，所以在中序遍历序列中的起止位置是[ri + 1, ie]，在后序遍历序列中的起止位置为：[pos + leftChildTreeNodeNum, poe - 1]；

按照上面的分析结果，边界弄清楚了，那么代码写起来也就方便了，代码如下所示：

/**
 * 递归解法
 *
 * @param inorder 中序遍历序列
 * @param postorder 后序遍历序列
 * @return 还原后的二叉树
 */
public TreeNode buildTree(int[] inorder, int[] postorder) {
    Map<Integer, Integer> indexContainer = new HashMap<>((int) (inorder.length / 0.75) + 1);
    for (int i = 0; i < inorder.length; i++) {
        indexContainer.put(inorder[i], i);
    }
    return buildTreeHelper(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1, indexContainer);
}

private TreeNode buildTreeHelper(int[] inorder, int is, int ie, int[] postorder, int pos, int poe,
        Map<Integer, Integer> map) {
    // 如果postorder为空，直接返回null
    if (ie < is || poe < pos) {
        return null;
    }
    // 获取根节点
    TreeNode root = new TreeNode(postorder[poe]);
    int ri = map.get(postorder[poe]);
    // 获取左子树的节点个数，这样就可以在后序遍历列表中确定左右子树
    int leftTreeNodeNum = ri - is;
    // 确定左右子树
    root.left = buildTreeHelper(inorder, is, ri - 1, postorder, pos, pos + leftTreeNodeNum - 1, map);
    root.right = buildTreeHelper(inorder, ri + 1, ie, postorder, pos + leftTreeNodeNum, poe - 1, map);
    return root;
}

五、总结一下

二叉树的还原至少需要知道三种遍历方式中的两种才可以正确还原，如果只知道其中一个，那么被还原出来的二叉树可能存在多个。其实还原二叉树这类题型倒是没什么难度，主要是需要弄清边界，理清二叉树的特性，那么问题将迎刃而解！

读完本文，你可以将文中代码直接粘贴到leetcode中就可以直接运行，涉及的三道题在这里再列一下：

• No.104 从前序与中序遍历序列构造二叉树
• No.889 根据前序和后序遍历构造二叉树
• No.106 从中序与后序遍历序列构造二叉树

欢迎读者评论交流~