第1节 数组理论基础

一、什么是数组

数组是一个固定长度的存储相同数据类型的数据结构，数组中的元素在内存中的存储方式表现为存储在一段连续的内存空间中，它是一种线性表数据结构。

它是最简单的数据结构之一，大多数现代编程语言都内置数组支持。由于数组给人的印象是十分简单的，所以很多读者都简单地认为了解即可。其实数组相关的算法题在思维上并不复杂，逻辑简单，但是在实现起来可能也存在一定的难度，所以也是需要好好掌握数组这种基本的数据结构，夯实好了基础，你会发现后续很多复杂的数据结构在底层实现上都有数组的身影。

本文将基于Java语言实现的数组，来介绍数组的基本理论基础。在第2节中将讲解leetcode中常见的数组相关的算法题。

二、数组的表现形式

2.1 一维数组

数组是一个固定长度的存储相同数据类型的数据结构，数组中的元素在内存中的存储方式表现为存储在一段连续的内存空间中。我们这里定义一个数组，如下图所示：

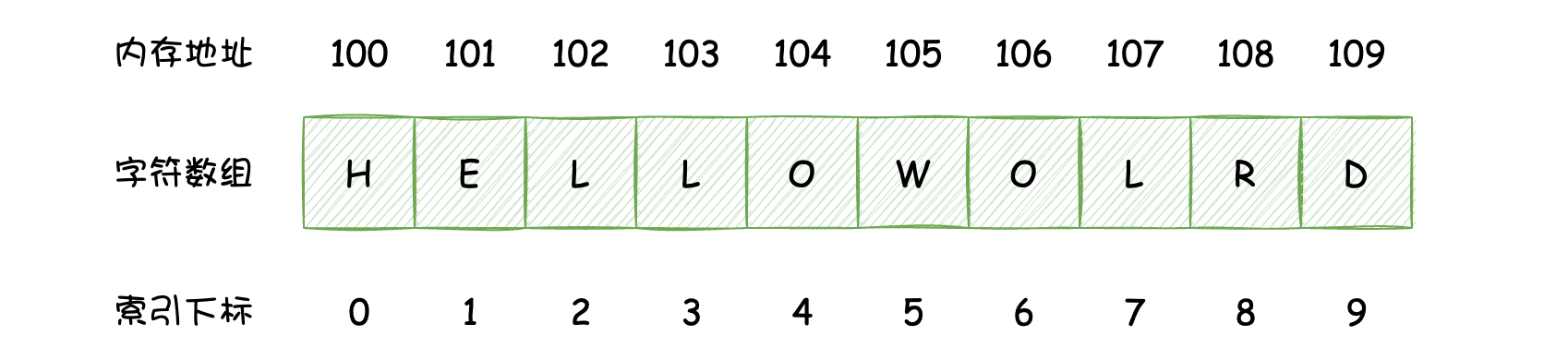
这里有两点需要说明：

• 这里的数组内存地址是虚拟描述的，是为了展现内存地址的连续性。
• 数组的索引下标都是从0开始的。

从图中可以看出，数组的两个特点：线性和连续性。

线性： 线性是指具有线性表一样的线性特征，即所有元素排成像一条线一样的结构，且所有的元素类型都是相同的，在方向上，每个元素只存在前后两个方向，无其他方向。除了数组是线性表结构外，我们熟知的队列、栈、链表等都是线性结构。

连续性： 数组具有线性表的连续性特征，具体表现在在数据存储上是连续不中断的，在物理内存空间中也表现为各元素之间紧密相连。这一点区别链式的线性表，比如链表，它在内存空间中一般不是紧密相连的，这点要区别开。

2.2 多维数组

2.1中介绍的数组只有一个维度，它的每个元素都是最基本的数据，它被称为一维数组。如果一个数组中的元素的类型还是一个数组的话，那么这样的数组表现出来的就是多维数组，这里以二维数组为例，如下图所示：

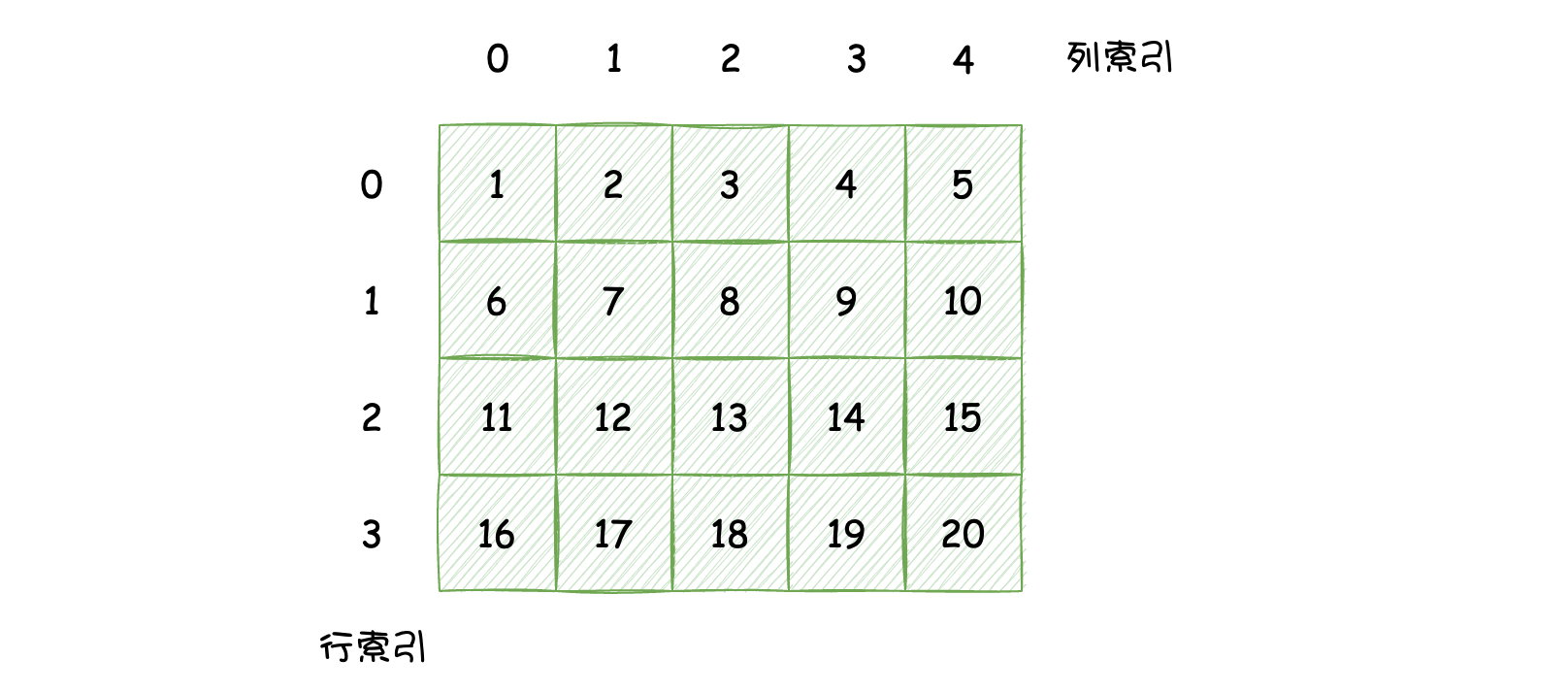
在行索引中，每个下标（0、1、2、3）指向的元素是一个子数组，每个子数组内部一共5个元素，其实这种二维数组在数学中称之为矩阵，它是由m行n列的数据构成的结构。

三维数组按照理论也可以想象，就是二维数组中的每个元素还是一个子数组，这样就构成了三维数组。多维数组以此类推。

2.3 数组在Java中的实现

在不同的编程语言中，数组实现方式存在一定的差异，这里Java为例，一维数组定义如下所示：

char[] helloWorld = new char[] {'H', 'E', 'L', 'L', 'O', 'W', 'O', 'R', 'L', 'D'};

上述的定义方式，就是在内存空间申请了连续的10个元素的内存空间，空间大小为元素个数*元素占用的字节数（这里暂不考虑对象的其他空间占用）。

二维数组定义和一维类似，如下所示：

int[][] array = new int[][] {
        {1, 2, 3, 4, 5},
        {6, 7, 8, 9, 10},
        {11, 12, 13, 14, 15},
        {16, 17, 18, 19, 20}
};

二维数组就是在内存中申请了4个元素的内存空间，每个空间里面存储一个数组，所占用的空间大小为每个数组元素占用空间之和。

三、数组的基本操作

数组和其他数据结构一样，都是用来存储数据的，数据存储的过程中必然会对数据进行操作，基本操作都是一样的，那就是增删改查。接下来，我们以一维数组为例分别阐述四种基本操作，为了体现代码的简易性，数组的操作中就不加入边界的判断了，读者在在实际的算法题中要充分考虑边界问题。

3.1 增：新增元素

我们在『2.3 数组在Java中的实现』中定义一维数组的时候，是确定了数组的中的元素，且直接为所有元素申请内存空间，其实还有其他的方式，比如一次性申请好内存空间，然后依次将元素存储到内存空间中，如下所示：

public static void main(String[] args) {
    char[] helloWorld = new char[10];
    helloWorld[0] = 'H';
    helloWorld[1] = 'E';
    helloWorld[2] = 'L';
    helloWorld[3] = 'L';
    helloWorld[4] = 'O';
    helloWorld[5] = 'W';
    helloWorld[6] = 'O';
    helloWorld[7] = 'R';
    helloWorld[8] = 'L';
    helloWorld[9] = 'D';
}

第一行代码中，我们申请了10元素的内存空间，然后依次向数组中添加元素，其实这是一种『尾部新增元素』的方式，是在数组的尾部新增元素，直到所有的位置都设置了元素。如下图所示：

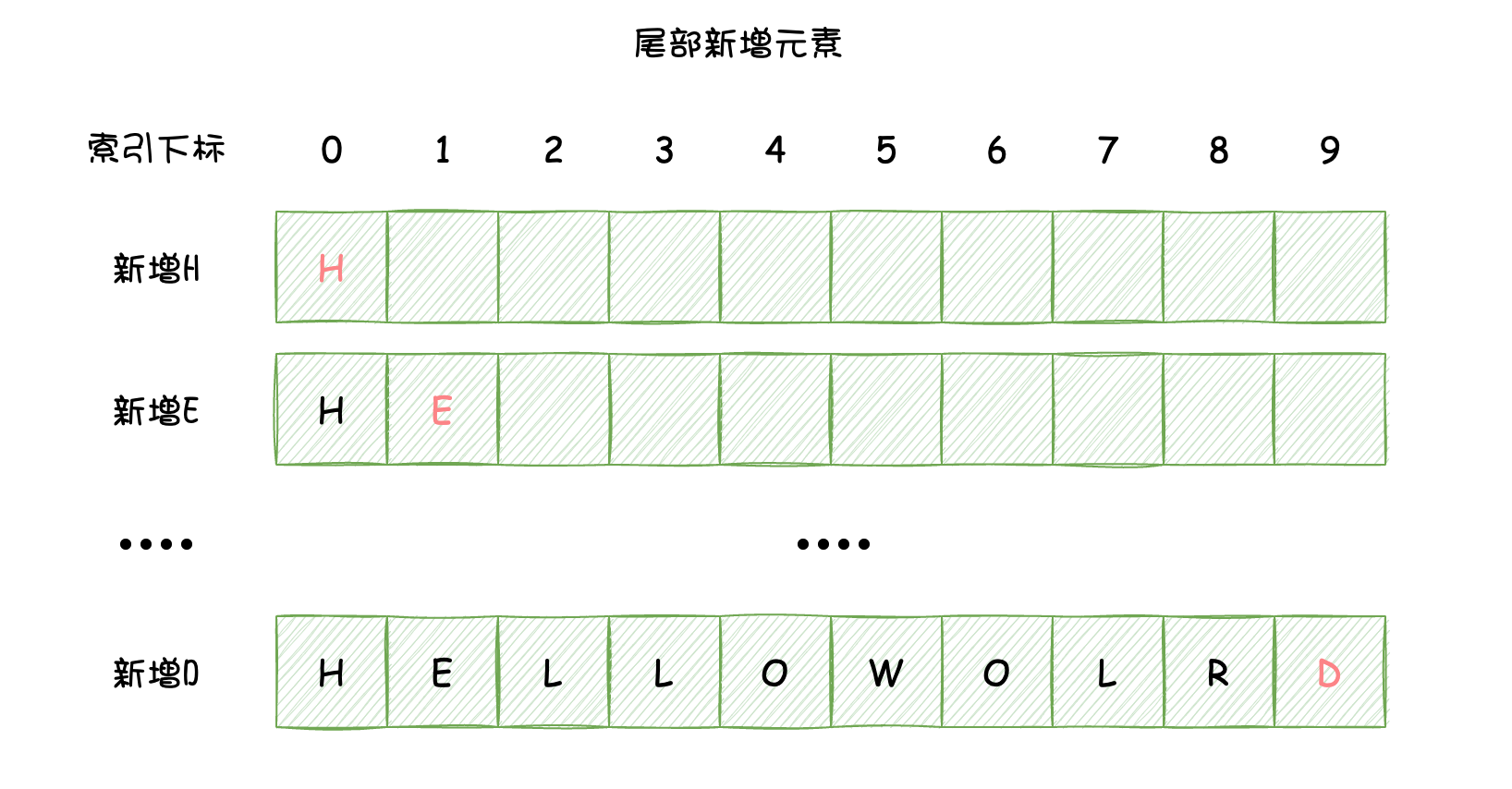
还有一种方式是『在指定位置新增元素』，这种方式新增元素就较为繁琐一些，涉及到了元素的挪动，如下图所示：

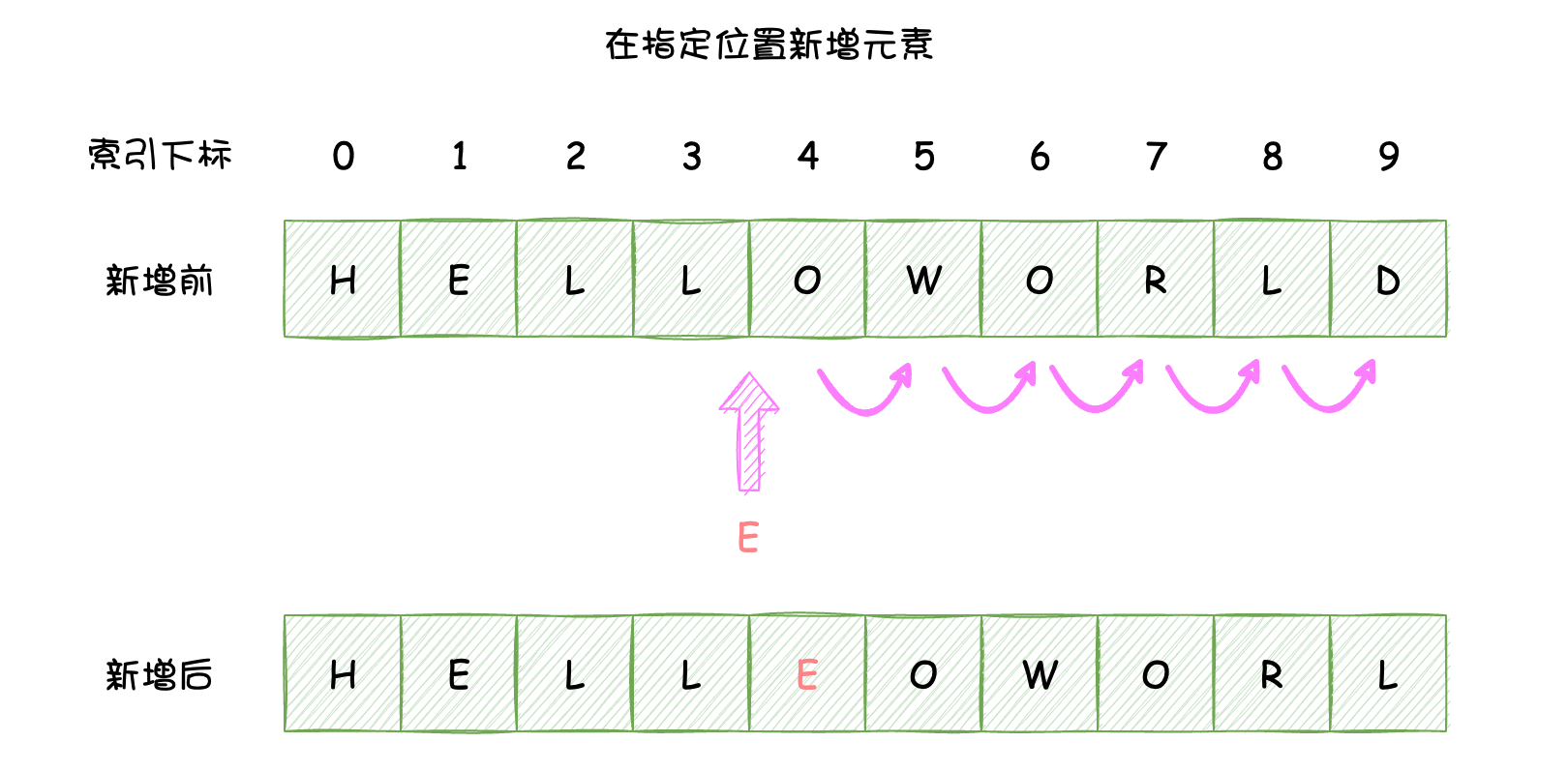
具体的代码实现方式如下所示：

public static void main(String[] args) {
    char[] helloWorld = new char[] {'H', 'E', 'L', 'L', 'O', 'W', 'O', 'R', 'L', 'D'};
    for (int i = helloWorld.length - 2; i >= 4; i--) {
        helloWorld[i + 1] = helloWorld[i];
        if (i == 4) {
            helloWorld[4] = 'E';
        }
    }
}

分析一下这两种新增元素的方式的时间复杂度，『尾部新增元素』和『在指定位置新增元素』的时间复杂度是不一样的，前者是在数组的尾部新增元素，不涉及元素的挪动，所以时间复杂度是O(1)，而后者涉及到了元素的挪动，它的时间复杂度和数据的挪动个数n相关，时间复杂度为O(n)。

3.2 删：删除元素

删除数组中的元素大致也可以分为两种方式：『删除尾部元素』和『删除指定位置元素』。我们已经分析了新增元素的两种方式，其实这两种删除方式和新增相反，当然他们也有相同的地方，那就是时间复杂度和新增元素的两种方式的复杂度是一样的，分别是O(1)和O(n)。

删除尾部元素： 数组的元素个数其实在申请空间的时候就已经确定了，且不能进行扩容或者缩容，所以在模拟数组在尾部删除元素其实就是将尾部元素的下标剔除，不再计入数组中即可，这个操作的时间复杂度是O(1)。

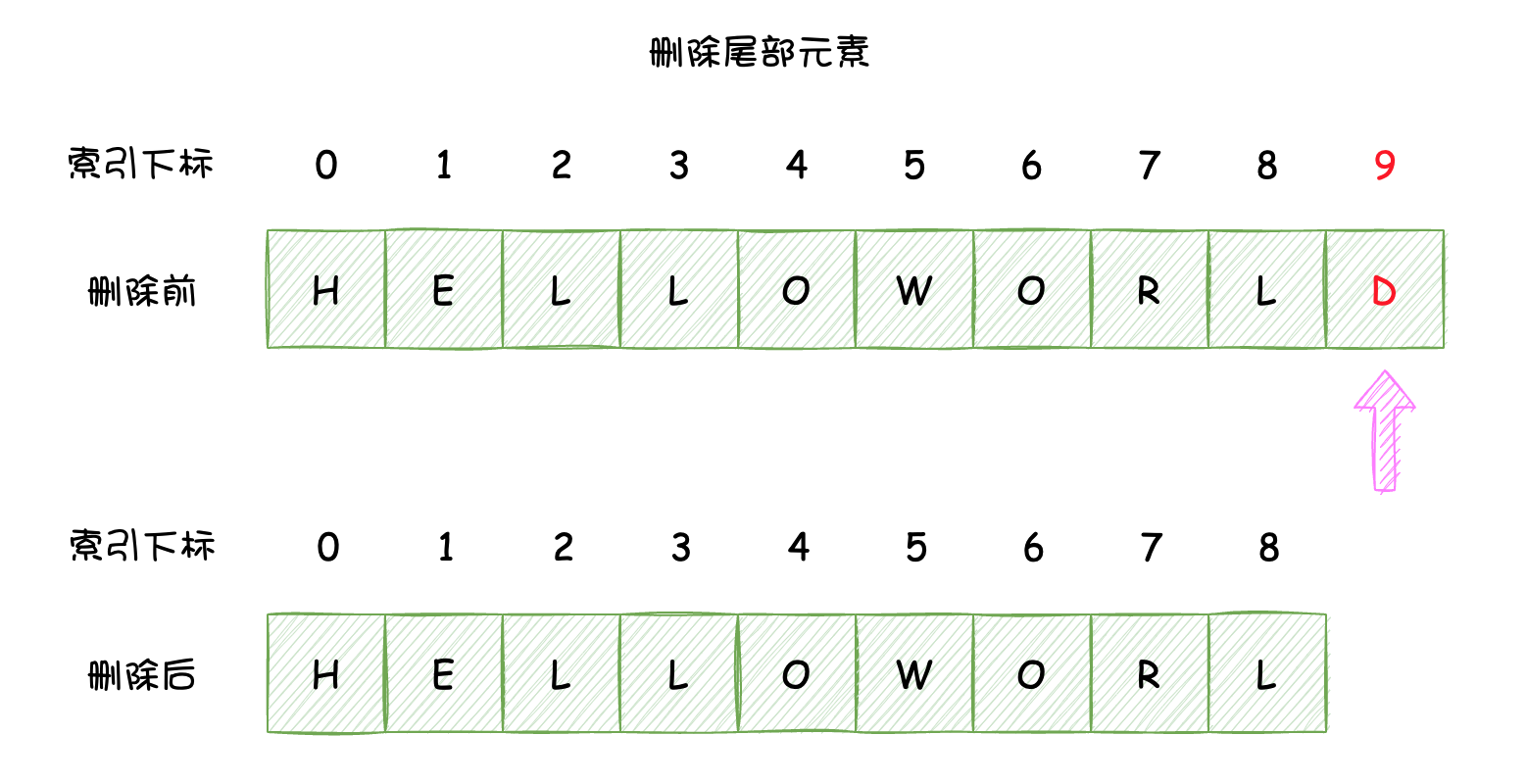
在Java中，数组中的元素不能被直接删除，通常是将不删除的元素拷贝到新的数组中，从而实现删除未拷贝的元素，『删除尾部元素』示例代码如下所示：

public static void main(String[] args) {
    char[] helloWorld = new char[] {'H', 'E', 'L', 'L', 'O', 'W', 'O', 'R', 'L', 'D'};
    helloWorld = Arrays.copyOf(helloWorld, helloWorld.length - 1);
    System.out.println(helloWorld);
}

上述代码中拷贝了除元素D以外的其他元素，并赋值给原来的helloWorld变量。

删除指定位置元素： 删除指定位置的元素，这也涉及了元素的挪动，时间复杂度为O(n)。如下图所示：

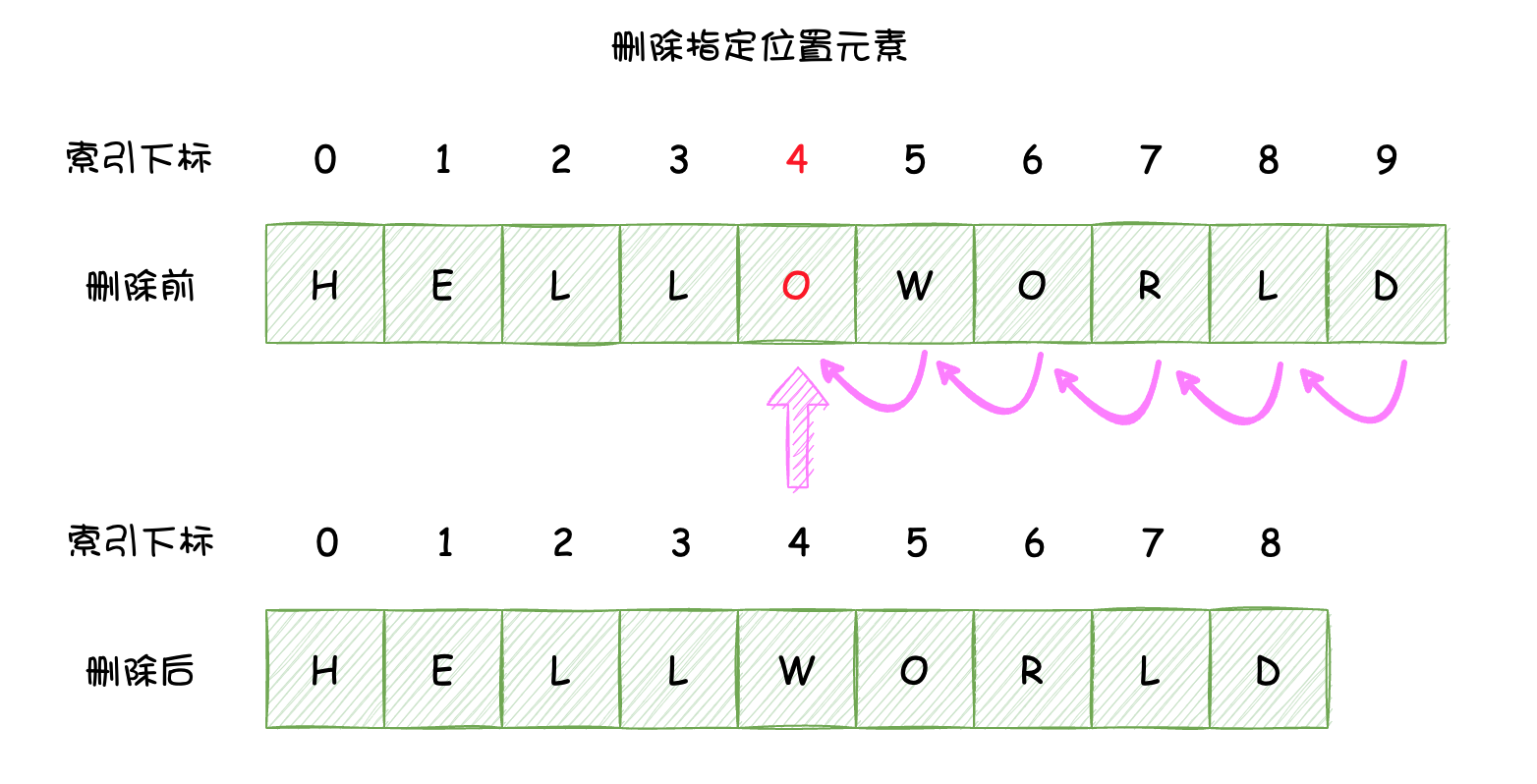
在Java中，数组中的元素不能被直接删除，通常是将不删除的元素拷贝到新的数组中，从而实现删除未拷贝的元素，『删除指定位置元素』示例代码如下所示：

public static void main(String[] args) {
    char[] helloWorld = new char[] {'H', 'E', 'L', 'L', 'O', 'W', 'O', 'R', 'L', 'D'};
    // 这里假设删除所以为4的元素，也就是O
    for (int i = 5; i < helloWorld.length; i++) {
        helloWorld[i -1] = helloWorld[i];
    }
    helloWorld = Arrays.copyOf(helloWorld, helloWorld.length - 1);
    System.out.println(helloWorld);
}

上述代码中假设删除的是索引为4的元素，那么从第5个元素开始，都向前移动一位，然后直接拷贝移动后的数组的前helloWorld.length - 1个元素即可。

3.3 改：修改元素

修改数组中的元素就相对比较简单了，直接将指定下标的元素替换成目标元素即可。修改操作不依赖于数组中元素个数，因此时间复杂度为 O(1)，如下图所示：

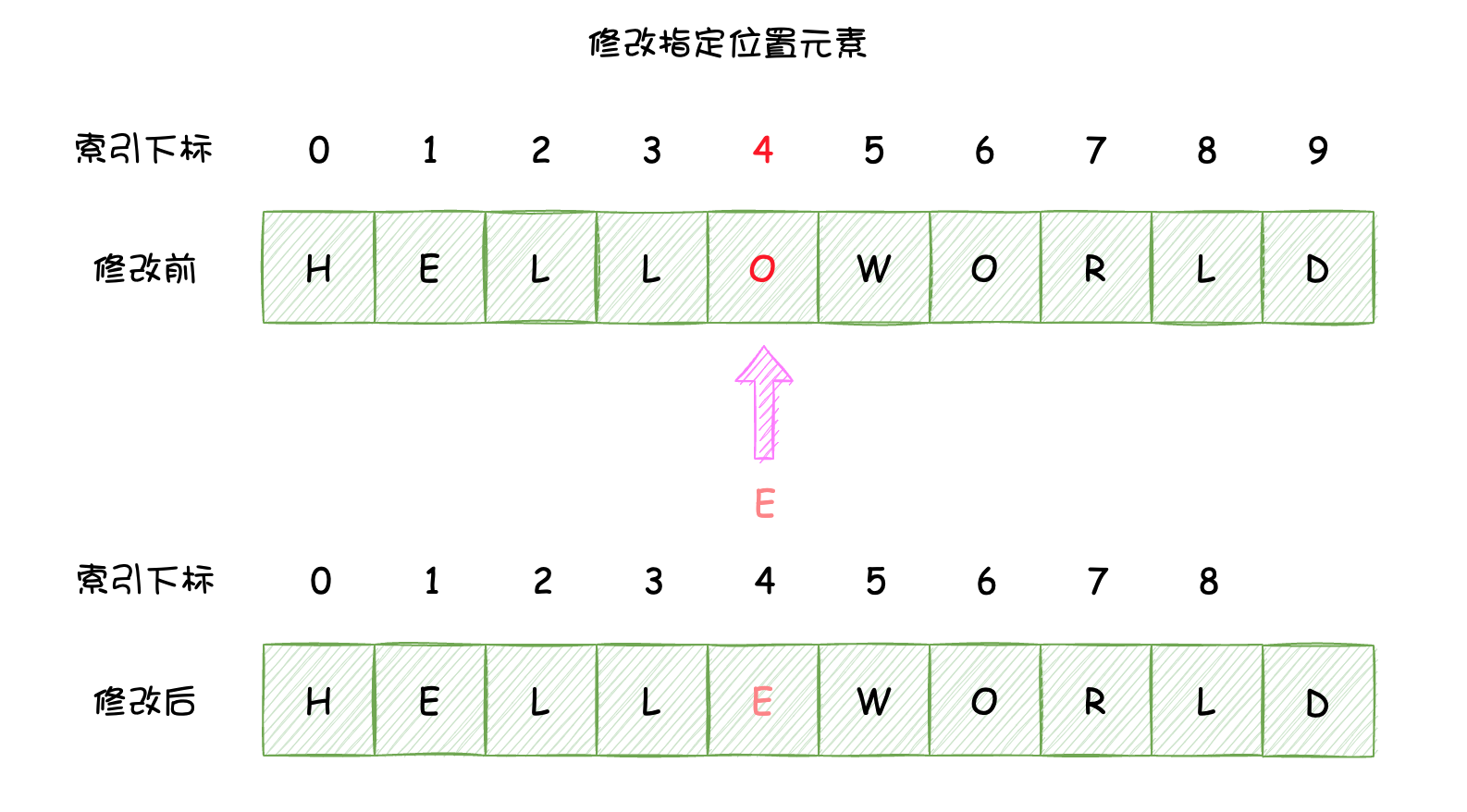
示例代码如下所示：

public static void main(String[] args) {
    char[] helloWorld = new char[] {'H', 'E', 'L', 'L', 'O', 'W', 'O', 'R', 'L', 'D'};
    helloWorld[4] = 'E';
    System.out.println(helloWorld);
}

3.4 查：访问元素

访问元素很简单，如果知道元素的下标，那么可以以O(1)的时间复杂度直接访问到该元素；如果不知道元素的下标，仅仅知道元素的值，那么需要对数组进行遍历才可能找到元素，这个时候最差的时间复杂度就是O(n)了。示例代码如下所示：

public static void main(String[] args) {
    char[] helloWorld = new char[] {'H', 'E', 'L', 'L', 'O', 'W', 'O', 'R', 'L', 'D'};
    // 直接访问已知的位置的元素，时间复杂度：O(1)
    System.out.println(helloWorld[4]);
    // 访问未知位置的第一个'O'元素，时间复杂度：O(n)
    for (int i = 0; i < helloWorld.length; i++) {
        if ('O' == helloWorld[i]) {
            System.out.println('O');
            break;
        }
    }
}

四、总结

数组是最简单、最基础的数据结构，它是实现其他数据结构的基础。在内存空间中，它表现为使用一组连续的内存空间来存储相同类型的元素，且内存空间不可扩容和缩容。它有如下特点：

• 数组的最大特点的支持随机访问；
• 数组访问元素、改变元素的时间复杂度为O(1)，在尾部插入、删除元素的时间复杂度也是O(1)，普通情况下插入、删除元素的时间复杂度为O(n)。