第2节 一文搞定单调栈算法题

栈（stack）是一种特殊的数据结构，但也是一种容易理解的数据结构，它的特点就是先进后出，生活中有很多栈的例子，比如装乒乓球的直筒，最先进入的球到达桶底，然后一个一个进入，最后进入的球在出桶的时候是第一出来，最先进去的是最后一个出来。本文所提到的单调栈其实就是在普通栈的基础上加上了单调的特性，栈内元素保持单调递增或者单调递减的特性。

一、单调栈解决的问题

本文主要利用单调栈来解决leetcode上的典型问题，其实它的应用范围倒是不广，主要解决的都是类似于leetcode上下一个更大元素的问题，本文将从这类问题出发，帮助大家掌握单调栈的应用技巧。主要题型如下所示：

序号	题目	类型	解法
739	每日温度	中等	单调栈
496	下一个更大元素 I	简单	单调栈
503	下一个更大元素 II	中等	单调栈
901	股票价格跨度	中等	单调栈
402	移掉K位数字	中等	单调栈
581	最短无序连续子数组	中等	单调栈
84	柱状图中最大的矩形	困难	单调栈
42	接雨水	困难	单调栈
316	去除重复字母	困难	单调栈

本文将从一个案例出发，确定基本的单调栈解题方法，后续的题目将应用这种方法来解答，通过多道题的训练后，相信读者肯定可以掌握单调栈的解题思路。

二、基础案例

本案例是leetcode上No.496 下一个更大元素 I的简单版本，题目描述如下：

给你一个数组nums，请返回一个等长的数组，这个等长数组对应于nums的相同位置存储着下一个更大元素，如果没有更大元素，请存储数值-1。假设nums的每个元素都不为负数。

案例：

比如输入数组为nums = [2,1,3,4,2]，那么返回数组[3,3,4,-1,-1]

解释：

数组nums的第一个元素2的下一个更大元素是3，第二个元素1的下一个更大元素是3，第三个元素3的下一个更大元素是4，第四个元素4没有下一个更大元素，第五个元素2同样没有下一个更大元素。

解法一：暴力法

其实题目理解起来很简单，就是找到数组中每个元素后面第一个比它大的元素，第一想到的解法就是暴力法，对每个元素进行遍历，然后再做一个内层遍历，找到第一个比它大的元素，设置到新数组的指定位置即可，如果没有，则设置-1。具体解法代码如下：

/**
 * 暴力解法：O(n^2)
 *
 * @param nums 数组
 * @return 输出数组
 */
public int[] nextGreaterElement(int[] nums) {
    int[] result = new int[nums.length];
    // 遍历到倒数第二个元素即可，最后一个元素直接赋值为-1
    for (int i = 0; i < nums.length - 1; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] > nums[i]) {
                result[i] = nums[j];
                break;
            }
            if (j == nums.length - 1) {
                result[i] = -1;
            }
        }
    }
    result[nums.length - 1] = -1;
    return result;
}

暴力解法通常很直接，也是最容易联想到的方法，本题暴力解法的时间复杂度是O(n^2)。

解法二：单调栈

找到数组nums每个元素的下一个更大元素，其实可以模拟到日常生活的站队的场景，将元素的大小抽象为人的身高，高个儿的人将挡住后面的人，从列队往后看，每个人下一个更高的人将一目了然，如下图所示：

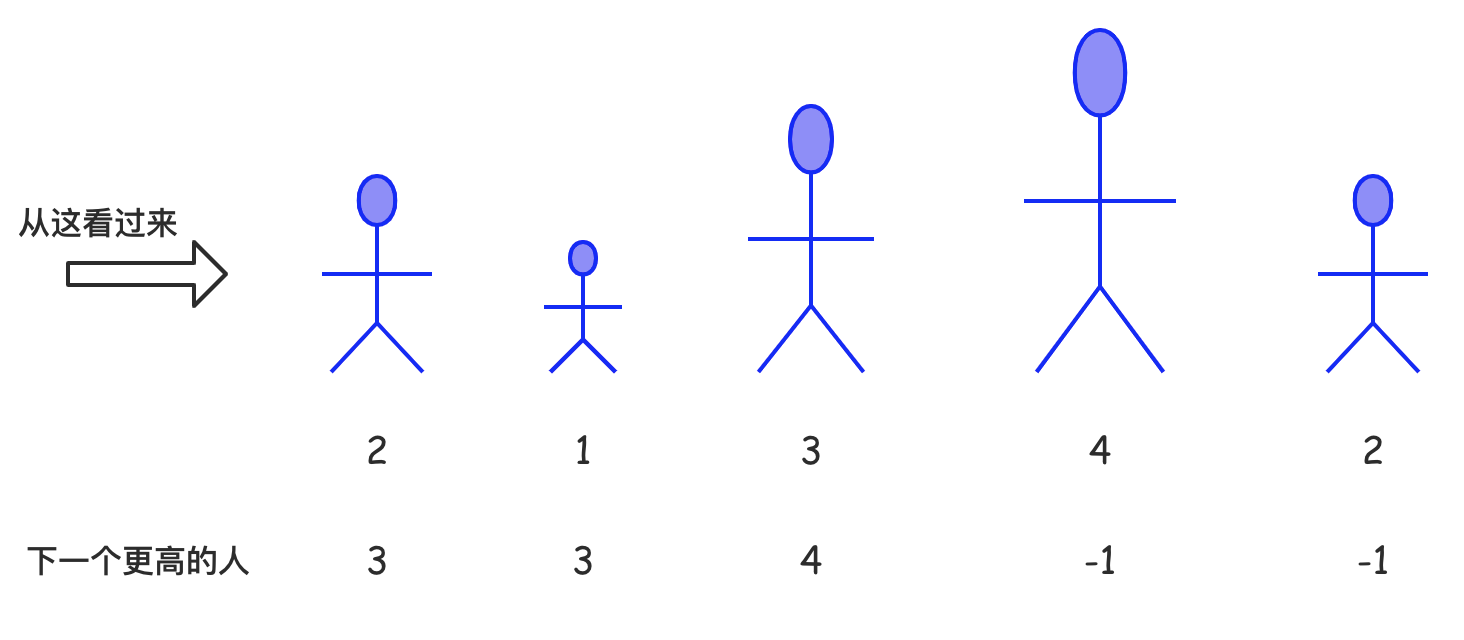
模拟站队的场景，相信大家应该很好理解了吧，那么有了这个场景，该如何使用单调栈来解决这个问题呢？想想我们是要解决什么问题，我们是需要找到某个元素的下一个更大元素，也就是队伍中某个人的下一个更高的人。其实队伍中每个人都有可能是站在他前面的人的下一个更高的人，如果某个人前面站了比自己高的人，那么他就不可能是别人的下一个更高的人了，因为他前面的人比他高，挡住了他。

我们从队伍的后面往前看，身高为2的人，它有可能是站在他前面的人的下一个更高的人，但是再看身高为4的人，那么身高为2的那个人就被淘汰掉了，因为4挡住了2，2不可能成为别人的下一个更高的人了，我们再看3，3比4矮，那么4就是3的下一个更高的人，但是3还是有可能是他前面人的下一个更高的人，我们再看1，1比3矮，3是1的下一个更高的人，再看2，2比1高，所以1被淘汰，淘汰掉1后，2后面就是3了，这个时候就得出2的下一个更高的人是3。

通过上面的解析得出，如果某个元素前面存在比他大的元素，那么这个元素就被淘汰了，如果比他小，那么可以继续留着和前面的人进行比较，这不就有点符合单调栈的思路了吗？栈底到栈顶单调递减，如下图所示：

我们从数组后面往前面遍历，如果栈为空，那么它自己就入栈，因为它有可能是它前面某个元素的下一个更大的元素，且它后面不存在比它更大的元素了。如果遍历到前面一个元素，如果别人比它大，那么它就出栈，因为它不可能是前面某个元素的下一个更大的元素了，如果前面的元素比它小，那么前面的元素也入栈，且入栈前的栈顶元素就是那个元素的下一个更大的元素。

有了图的解析，相信大家已经明白了，直接上代码：

public int[] nextGreaterElement(int[] nums) {
    int[] result = new int[nums.length];
    Stack<Integer> stack = new Stack<>();
    for (int i = nums.length - 1; i >= 0; i--) {
        while (!stack.isEmpty() && nums[i] >= stack.peek()) {
            stack.pop();
        }
        result[i] = stack.isEmpty() ? -1 : stack.peek();
        stack.push(nums[i]);
    }
    return result;
}

代码写起来比较简单，从代码中可以看出，这个时间复杂度是O(n)，因为对每个元素进行了一次压栈和弹栈，虽然加上while循环，但是while循环里面并没有对数组有任何的操作，仅仅就是把比当前元素小的元素全部弹出（因为小元素不可能是别人的下一个更高元素），所以时间复杂度是O(n)。

总结一下单调栈问题的解题套路：遍历数组，构建单调递增或者递减的栈，这点很重要，因为后面的题目基本都是单调栈的应用，都是通过构建单调递增或者递减的栈来解决问题的。

三、leetcode实战练习

3.1 每日温度 中等

我们趁热打铁，一起来看下leetcode第739题：每日温度，是一道典型的单调栈类型的问题，和上面的基础案例如出一辙，题目如下：

这道题和基础案例中的唯一区别就是存储的内容不一样，基础案例存储的是下一个更大元素，而本题存储的是下一个更大元素与当前元素的距离。解法一样，从数组的尾部开始遍历，构建单调栈。直接上代码：

public int[] dailyTemperatures(int[] temperatures) {
    int[] result = new int[temperatures.length];
    Stack<Integer> stack = new Stack<>();
    for (int i = temperatures.length - 1; i >= 0; i--) {
        while (!stack.isEmpty() && temperatures[i] >= temperatures[stack.peek()]) {
            stack.pop();
        }
        // 求取距离就是两索引的差
        result[i] = stack.isEmpty() ? 0 : stack.peek() - i;
        // 存储当前元素的索引
        stack.push(i);
    }
    return result;
}

掌握了单调栈类型的问题解法后，这类题目的思路是不是一下就打开了？嗯，是的，看似是的，但是如果现在让你去做剩下的单调栈的题目，也不一定做的出来。很多写算法文章作者，都只喜欢举一两个典型的例子，但是往往一两个例子并不能帮助读者真正掌握，索性把这类题目全部讲解了，再反复练习领会，应该效果会更好点，这也是我要和读者一起把剩下的单调栈题目挨个解决的原因。

3.2 下一个更大元素 I 简单

本道题摘自leetcode第496题：下一个更大元素 I，是一道简单题，如果没有前面两个案例的讲解，那你是否能想到使用单调栈来做呢？这道题的暴力解法很容易想到，那就是遍历数组nums1，然后根据nums1中的每个元素去nums2中找到该元素的位置，并从那个位置往后遍历，找到下一个更大的元素值。暴力的解法通常都很直接，所以这里不再写暴力解法的代码，直接使用单调栈来解决这道题。

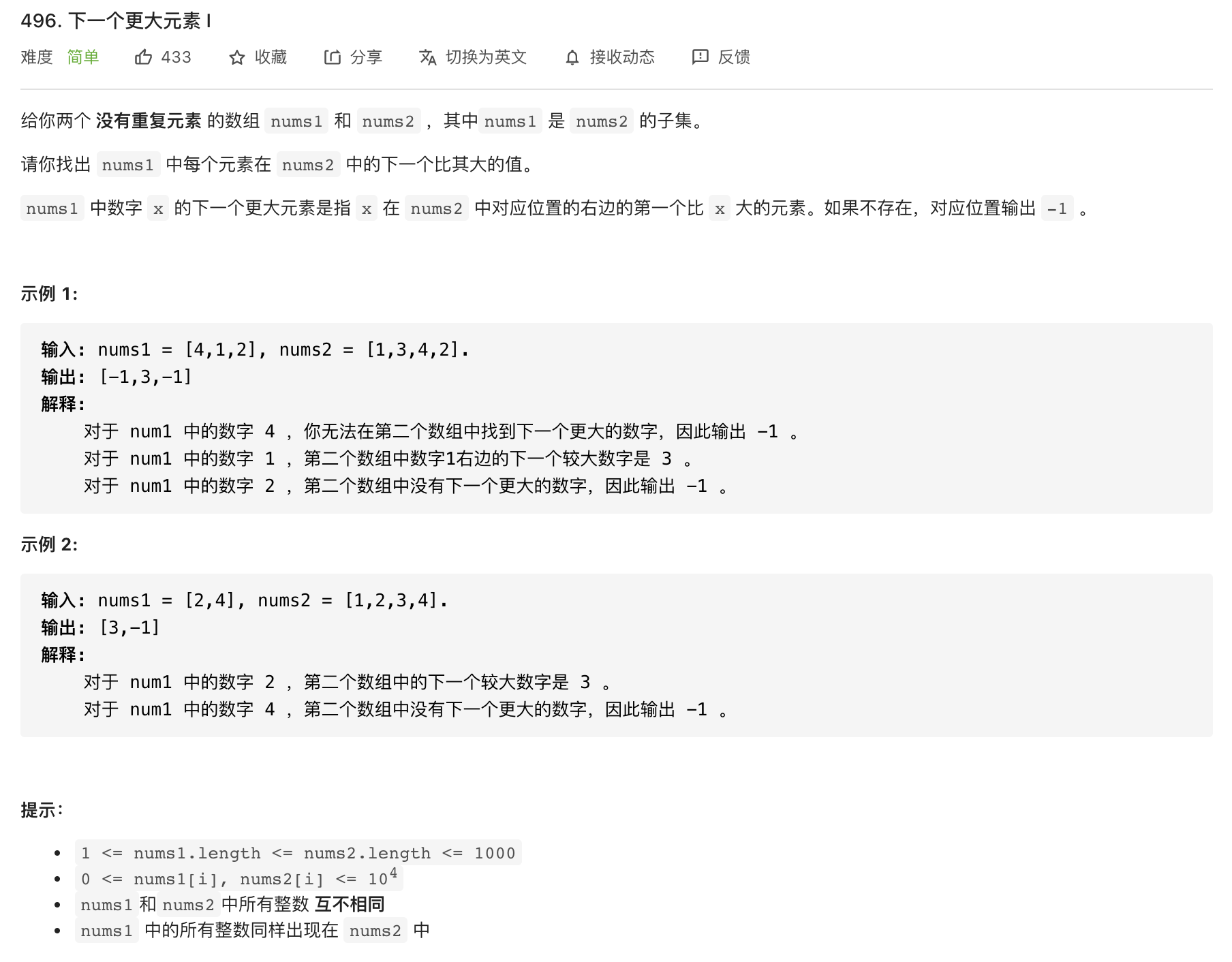
题目中有一个重要的提示就是两个数组中没有重复元素，且nums1是nums2的子集，所以这里联想到在遍历nums2求每个元素的下一个更大元素的时候，可以考虑使用Map来记录这个关系，而不是和前面几题一样，使用数组来记录，这样做的好处是Map通过key来获取元素的时间复杂度是O(1)，如果不使用Map，那还得记录nums1中每个元素在nums2中的索引，这样就麻烦了点。代码如下所示：

/**
 * 使用map记录nums2中每个元素和下一个更大元素的关系：O(n)
 *
 * @param nums1 数组1
 * @param nums2 数组2
 * @return 数组
 */
public int[] nextGreaterElement2(int[] nums1, int[] nums2) {
    // 设置一个Map来存储nums2中每个元素和它下一个更大元素的关系
    Map<Integer, Integer> map = new HashMap<>((int) (nums2.length / 0.75) + 1);
    Stack<Integer> stack = new Stack<>();
    for (int i = nums2.length - 1; i >= 0; i--) {
        while (!stack.isEmpty() && nums2[i] > stack.peek()) {
            stack.pop();
        }
        // 使用map将nums2中的每个元素与其下一个更大元素关联起来
        map.put(nums2[i], stack.isEmpty() ? -1 : stack.peek());
        stack.push(nums2[i]);
    }
    // 遍历nums1，下一个更大元素
    for (int i = 0; i < nums1.length; i++) {
        nums1[i] = map.get(nums1[i]);
    }
    return nums1;
}

这里说明一点：代码Map<Integer, Integer> map = new HashMap<>((int) (nums2.length / 0.75) + 1);中，创建HashMap对象的时候指定了HashMap的初始化容量大小，这样做的好处是减少扩容带来的性能损耗。至于为何容量设置为(int) (nums2.length / 0.75) + 1，可以参考笔者的另一篇文章《深入理解JDK7 HashMap》，这里不过多介绍，读者也可以不去设置初始化容量，问题不大。

其实单调栈问题解题思路大多都是一样的，有些题目稍微改变一下形式就可以了，趁热打铁，我们继续往下看。

3.3 下一个更大元素 II 中等

接下来这道题也是一道经典的单调栈的问题，这里提到了循环数组，其实它就是首尾相连的一种特殊数组，这里需要读者养成一种反射弧，如果提到循环、首尾相连等字样，应该能立马联想到模运算（求余运算），也就是下标 % 长度，本题中就用到了模运算。

本题中的循环数组[1,2,1]使用下图表示：

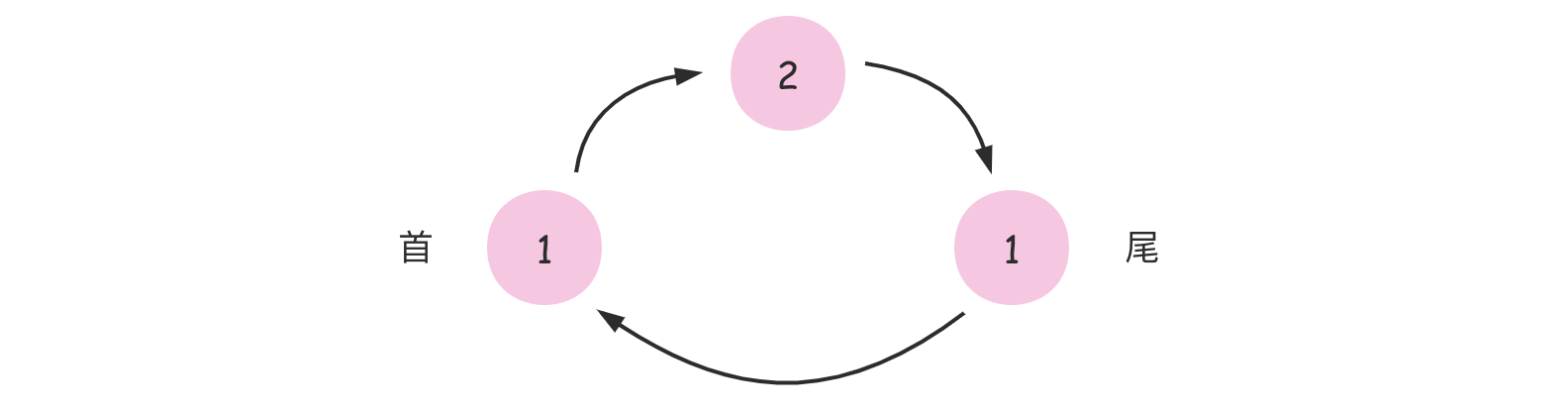
读完题目候，你是否有这种感觉？之前的题目，每个元素的下一个更大元素只会出现在其右侧，从这道题看，某个元素的下一个更大元素还有可能出现在其左侧，因为循环一圈回来之后，找到的第一个更大元素完全可能就出现在其左侧。那这道题该如何解答？

在数据结构理论中，常常使用模运算来模拟环状的数据结构，循环数组[1,2,1]的长度为3，索引为3的元素是1，因为3 % 3 = 0，索引为3的元素其实就是0号元素，所以处理循环数组的索引直接使用模运算：index % nums.length即可。

有了这个理论的支持，我们做这道题就方便多了，对于这道题，遍历数组，我们遍历两遍就可以把所有的元素的下一个更大元素找出来，其实最简单的方式就是将数组进行翻倍处理，这里的翻倍不是扩容为两倍，而是遍历两遍就可以了，采用模运算的方式来处理，不是真正地翻倍。其核心部分还是使用单调栈的解题思路，从数组后往前遍历，倒序入栈，正序出栈。这里处理后，元素不仅仅可以和自己右边的元素进行比较，还可以与左边的元素进行比较。代码如下所示：

/**
 * 环状数组常用的做法就是就是使用模的形式来模拟数组有环，实际是没有增加任何空间
 *
 * @param nums 数组
 * @return 数组
 */
public int[] nextGreaterElements(int[] nums) {
    int[] result = new int[nums.length];
    Stack<Integer> stack = new Stack<>();
    for (int i = nums.length * 2 - 1; i >= 0; i--) {
        while (!stack.isEmpty() && nums[i % nums.length] >= stack.peek()) {
            stack.pop();
        }
        result[i % nums.length] = stack.isEmpty() ? -1 : stack.peek();
        stack.push(nums[i % nums.length]);
    }
    return result;
}

这道题使用单调栈解法其实很简单，思想是一模一样的，需要记住的两个知识点：一是，使用模运算来模拟环状数组，二是翻倍，将环状拉直，因为2圈就可以拉直为线性的方式来处理。

3.4 股票价格跨度 中等

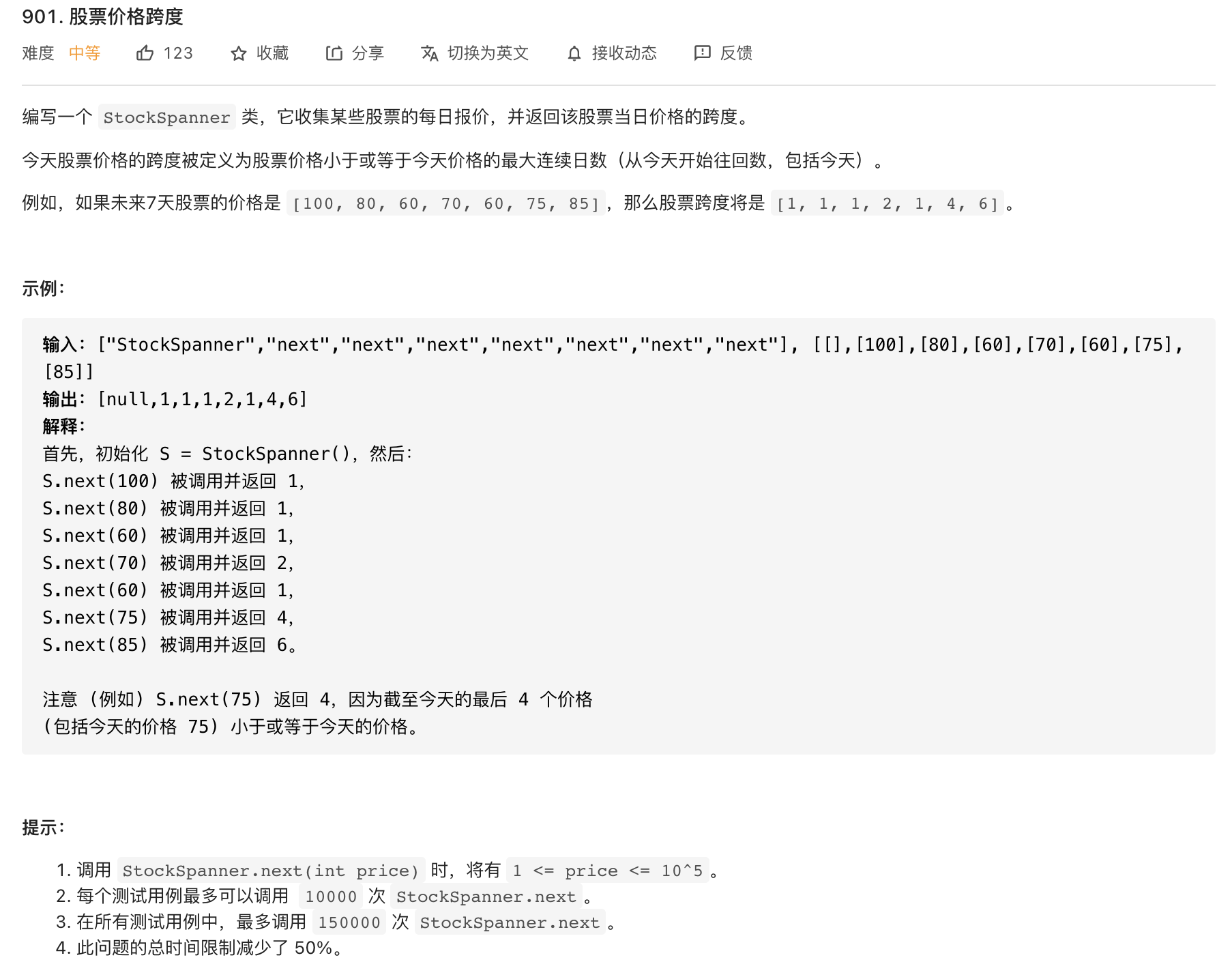
这道题拿到手第一感觉是读不懂，笔者没有玩过股票，这些股市的概念也基本没有机会接触到，但是我们可以将题目认真分析，转化为我们程序员能读懂的内容。其实从数组角度来看，就是从左到右找到每个元素左侧连续小于等于它的元素个数，包括自身，题目中的数组[100, 80, 60, 70, 60, 75, 85]，我们拿这个分析下：

• 第一个元素100，它左侧连续小于等于100的只有它自身，所以返回1；
• 第二个元素80，它左侧连续小于等于80的只有它自身，所以返回1；
• 第三个元素60，它左侧连续小于等于60的只有它自身，所以返回1；
• 第四个元素70，它左侧连续小于等于70的只有60和它自身，所以返回2；
• 第五个元素60，它左侧连续小于等于60的只有它自身，所以返回1；
• 第六个元素75，它左侧连续小于等于75的有60、70、60和它自身，所以返回4；
• 第七个元素85，它左侧连续小于等于85的有80、60、70、60、75和它自身，所以返回6；

分析到这里的话，也许可以想到使用暴力的解法，从后往前遍历，找到小于等于当前元素的个数，但是这道题是一道设计题，和之前的解法有点点区别，但是不大。我们试想下，如果某个元素w前面所有的元素都比它小，那么它后面的元素y，只要判断y与w的大小就行，如果w小于等于y，说明w前面的都小于等于y，将w前面元素的跨度加上w到y的跨度，那么就可以计算出y的跨度，那么这么算的话，就可以利用单调栈来解决这个问题。

为了把问题的解决办法说清楚，我们还是通过画图的方式来说明：

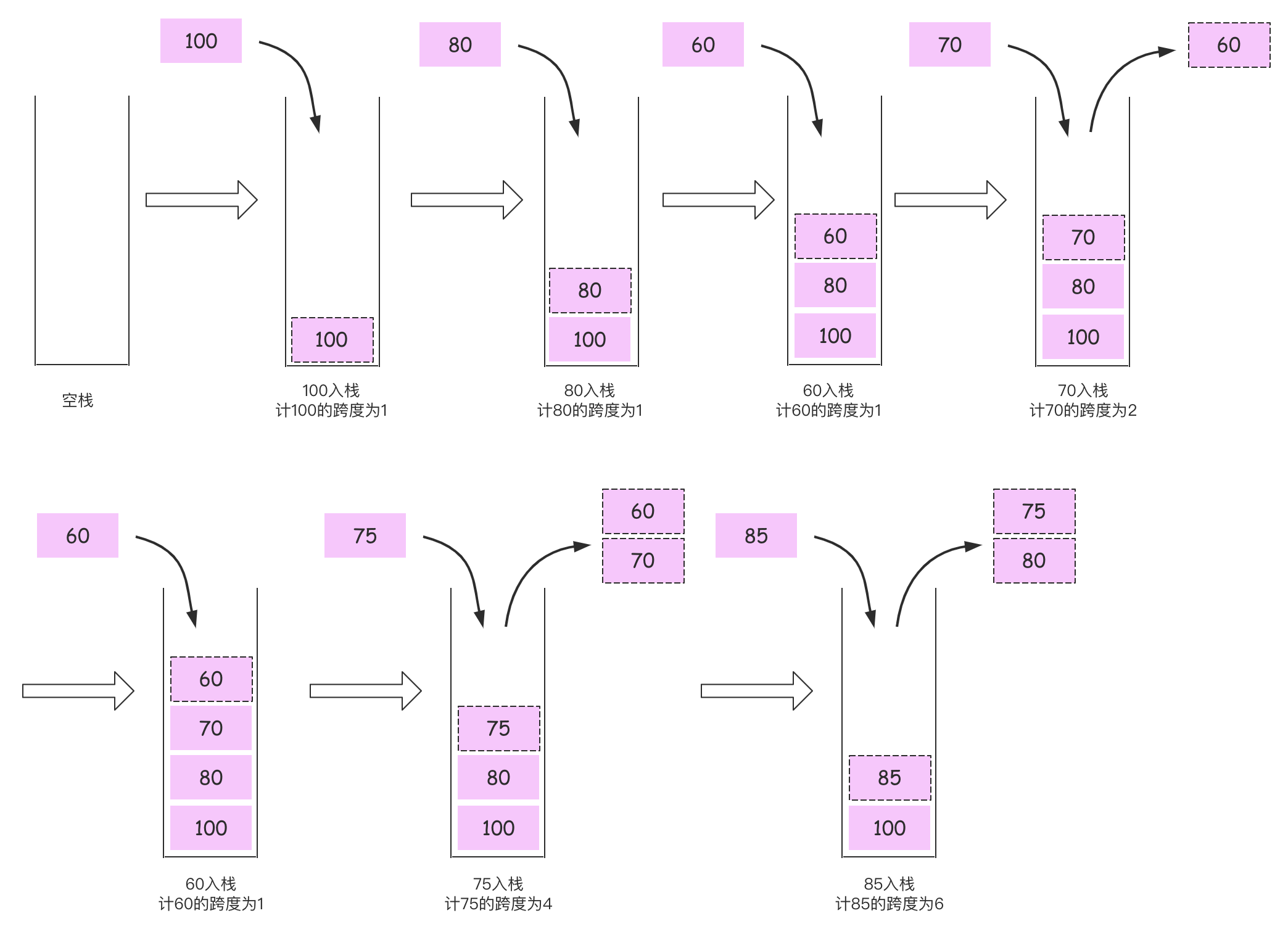
这里使用文字来辅助描述：

• 第一步：100入栈，此时100的跨度仅仅包含自身，跨度为1；
• 第二步：80入栈，100 > 80，80的跨度仅仅包含自身，跨度为1；
• 第三步：60入栈，80 > 60，60的跨度仅仅包含自身，跨度为1；
• 第四步：70入栈，60 < 70，80 > 70，70的跨度包含60和自身，跨度为2（将60的跨度累加起来），此时60应该出栈，因为70后面的元素，如果大于等于70，那么肯定大于60，这个时候70的跨度已经把60包含进去了，所以后面大于等于70的元素，小于80的元素，肯定把60包含进去了，所以60已经没有意义了；如果后面的元素小于70，那么60也起不到作用，因为被70隔开了；
• 第五步：60入栈，此时60的跨度仅仅包含自身，跨度为1；
• 第六步：75入栈，此时60和70都应该出栈，道理和第四步一样，75的跨度为4，分别累加了70的跨度2和60的跨度1，再加上自身1，所以跨度是4；
• 第七步：85入栈，此时75和80都应该出栈，道理和第四步一样，75的跨度为4，80的跨度为1，再加上自身，所以跨度是6。

其实这里还需要一个栈来记录跨度，这两个栈元素个数应该是一样的，一一对应的，分别记录每个元素的跨度，说到这里，应该很好理解了吧？我们一起来看下代码：

public class StockSpanner {
	
	/**
     * 栈priceStack和widthStack分别用来记录元素和跨跨度
     */
    private final Stack<Integer> priceStack;
    private final Stack<Integer> widthStack;

    public StockSpanner() {
        this.priceStack = new Stack<>();
        this.widthStack = new Stack<>();
    }

    public int next(int price) {
    	// 跨度至少为1，就是自身，所以这里是1，如果不包含自身，那么这里就是0
        int width = 1;
        while (!priceStack.isEmpty() && priceStack.peek() <= price) {
            priceStack.pop();
            width += widthStack.pop();
        }
        priceStack.push(price);
        widthStack.push(width);
        return width;
    }
}

只要把问题分析清楚了，代码写起来还是很简单的，核心的next方法内部使用的还是单调栈的思想。分析一下复杂度，时间复杂度还是O(n)，n为调用next方法的次数，空间复杂度也是O(n)。

3.5 移掉K位数字 中等

接下来这道题来自leetcode的第402道：移掉K位数字，也是一道经典的单调栈类的问题。

分析题目：

还是取案例中的两个数字字符串来进行分析，对于第一个数字字符串1432219，假如让你移除一位数字，你会移除哪一个？我们一起来分析下：

• 移除1，剩下的变成了432219；
• 移除4，剩下的变成了132219；
• 移除3，剩下的变成了142219；
• 移除2，剩下的变成了143219；
• 移除9，剩下的变成了143221。

一目了然，得出的结论是移除4最好，剩下的内容组成的数字最小。

这是为什么呢？其实是有数学规律的，这里提出数学中的两个概念：高位数和低位数（个、十、百、千、万，从低位到高位），且这里提供两个数来进行分析，分别是1234987和9871234我们分析如下：

• 对于一个数字字符串，我们从左向右遍历，需要一个容器记录每个遍历的过的数字；
• 对于这种高位递增的数1234987，我们肯定要保证高位数尽量小，因为删除一个高位数，如1，那么2顶上来，得出的结果234987肯定比删除2得出的结果134987要大，所以得出结论：高位递增的数要尽量保证高位数小，尽量删除低位的数；
• 对于这种高位递减的数9871234，我们同样要保证高位数尽量小，所以删除9的后得出的结果要比删除8得出的结果更小，所以得出结论：高位递减的数要尽量保证高位数小，尽量删除高位的数；
• 经过上面的分析，我们基本可以确定需要使用栈来充当这个容器了。当遍历每一个数字的时候，如果当前数字比栈顶数字大，是递增，那么就可以直接入栈，因为下一个数字有可能比当前的大；如果当前数字比栈顶的小，那么就需要将栈顶的元素弹出删除，因为这个栈顶元素既是递增的最后一个数字，也是递减的第一个数字，是一个尖峰，再删除过程中记录删除的个数或者将k - 1，当删除了所有k个数字后，就得出了结果。

需要注意的两点是，一是，数字字符串不能以0开头，这个可以再入栈的是进行检查，如果入栈的是0，且栈为空的时候，那么这个0是不入栈的，因为0作为栈底元素的话，那么是没有机会出栈的，因为它始终最小；或者是处理完毕后，最后结果以0开头，把0去掉即可，当然如果最后只有一个0的话，那就不去掉。二是，遍历完毕后，k个数字没有移除完，比如数字123456789，移除3个数字，按照上面的分析，得出的结果还是123456789，出现这种情况是因为移除部分数字后，得出的结果是一个高位递增的数，所以无法再移除了，这个时候，只要出现这种情况，将低位的数字移除掉剩余个数即可，可以仔细想想这一个特殊点。

分析完毕直接上代码：

/**
 * 移除字符串中K个数字
 *
 * @param num 数字字符串例如1432219
 * @param k 移除K个数字
 * @return 最小数字
 */
public String removeKdigits(String num, int k) {
    // 处理特殊情况
    if (k == num.length()) {
        return "0";
    }
    // 使用单调栈思想来解题
    Stack<Character> stack = new Stack<>();
    for (int i = 0; i < num.length(); i++) {
        while (k > 0 && !stack.isEmpty() && num.charAt(i) < stack.peek()) {
            stack.pop();
            k--;
        }
        // 这里做一个特殊处理，防止首位为0的入栈
        if (num.charAt(i) != '0' || !stack.isEmpty()) {
            stack.push(num.charAt(i));
        }
    }
    // 如果没有完成所有K个数字的移除，那么直接移除低位数，因为出现没有移除完的情况是因为一直再递增
    while (k > 0 && !stack.isEmpty()) {
        stack.pop();
        k--;
    }
    return stack.size() == 0 ? "0" : stack2String(stack);
}

/**
 * 将一个不为空的stack内的元素转换成字符串
 *
 * @param stack 栈
 * @return 字符串
 */
private String stack2String(Stack<Character> stack) {
    StringBuilder result = new StringBuilder();
    while (!stack.isEmpty()) {
        result.insert(0, stack.pop());
    }
    return result.toString();
}

时间复杂度和空间复杂度都是O(n)。

3.6 最短无序连续子数组 中等

这道题选自leetcode第581题：最短无序连续子数组，是一道经典的单调栈问题。

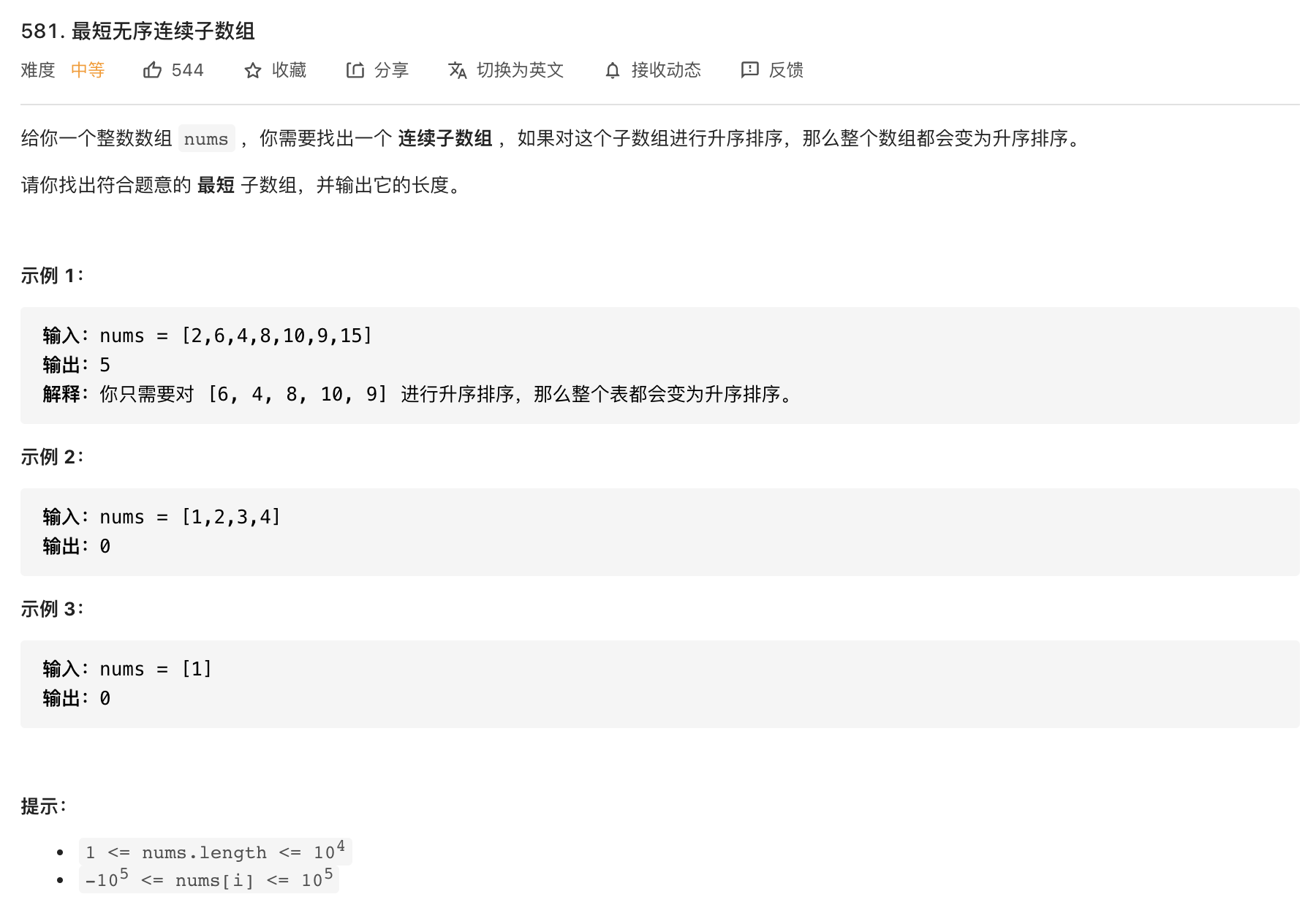
其实解决这道题的方法有很多，比如双指针法，将入参数组nums拷贝一份，记为nums2，然后将进行排序，然后对比两个数组，使用双指针从左和从右分别遍历，找到第一次不一样的位置索引，这样就可以计算出长度。这是一个常规解法，不再过多介绍，读者们看下面代码就明白了。

/**
 * 排序+双指针算法：O(nlogn)
 *
 * @param nums 数组
 * @return 最短无序连续子数组长度
 */
public int findUnsortedSubarray(int[] nums) {
    int[] nums2 = nums.clone();
    Arrays.sort(nums2);
    int start = nums2.length;
    int end = 0;
    for (int i = 0; i < nums2.length; i++) {
        if (nums[i] != nums2[i]) {
            start = Math.min(start, i);
            end = Math.max(end, i);
        }
    }
    return end - start >= 0 ? end - start + 1 : 0;
    }

这里着重介绍单调栈的解法，其实思路和上面的类似，都是为了找到最短无序连续子数组的左右边界，那么该如何使用单调栈来解决这个问题呢？

根据题意，希望找到最短无序连续子数组，然后对这个数组进行排序后就可以使整个数组处于一个升序的状态，那么其实通过构建一个单调递增栈和单调递减栈来解决这个问题。

• 从左向右遍历，构建单调递增栈，找到自始至终没有出栈的最大索引left；
• 从右向左遍历，构建单调递减栈，找到自始至终没有出栈的最小索引right；
• 左边的索引找到最大值，右边的索引找到最小值，这样囊括出来的数组肯定是最短无序连续子数组。

篇幅原因，这里不再画图，直接看代码，相信读者都会看懂：

/**
 * 单调栈解法：O(n)
 *
 * @param nums 数组
 * @return 最短无序连续子数组长度
 */
public int findUnsortedSubarray(int[] nums) {
    int left = nums.length - 1;
    int right = 0;
    // 单调递增栈
    Stack<Integer> incrementalStack = new Stack<>();
    for (int i = 0; i < nums.length; i++) {
        while (!incrementalStack.isEmpty() && nums[incrementalStack.peek()] > nums[i]) {
            left = Math.min(left, incrementalStack.pop());
        }
        incrementalStack.push(i);
    }
    // 单调递减栈
    Stack<Integer> decreasingStack = new Stack<>();
    for (int i = nums.length - 1; i >= 0; i--) {
        while (!decreasingStack.isEmpty() && nums[decreasingStack.peek()] < nums[i]) {
            right = Math.max(right, decreasingStack.pop());
        }
        decreasingStack.push(i);
    }
    return right > left ? right - left + 1 : 0;
}

这个单调栈解法的时间复杂度是O(n)。

相信大家看到这里，把上面的题目都练习了，肯定对单调栈已经有所了解了，接下里，我们再接再厉，趁热打铁，一起来做几道困难的题。

3.7 柱状图中最大的矩形 困难

这道题选自leetcode第84题：柱状图中最大的矩形，在leetcode中标记为困难题，读者看到困难也别担心，我们利用单调栈也能轻松地解决它。

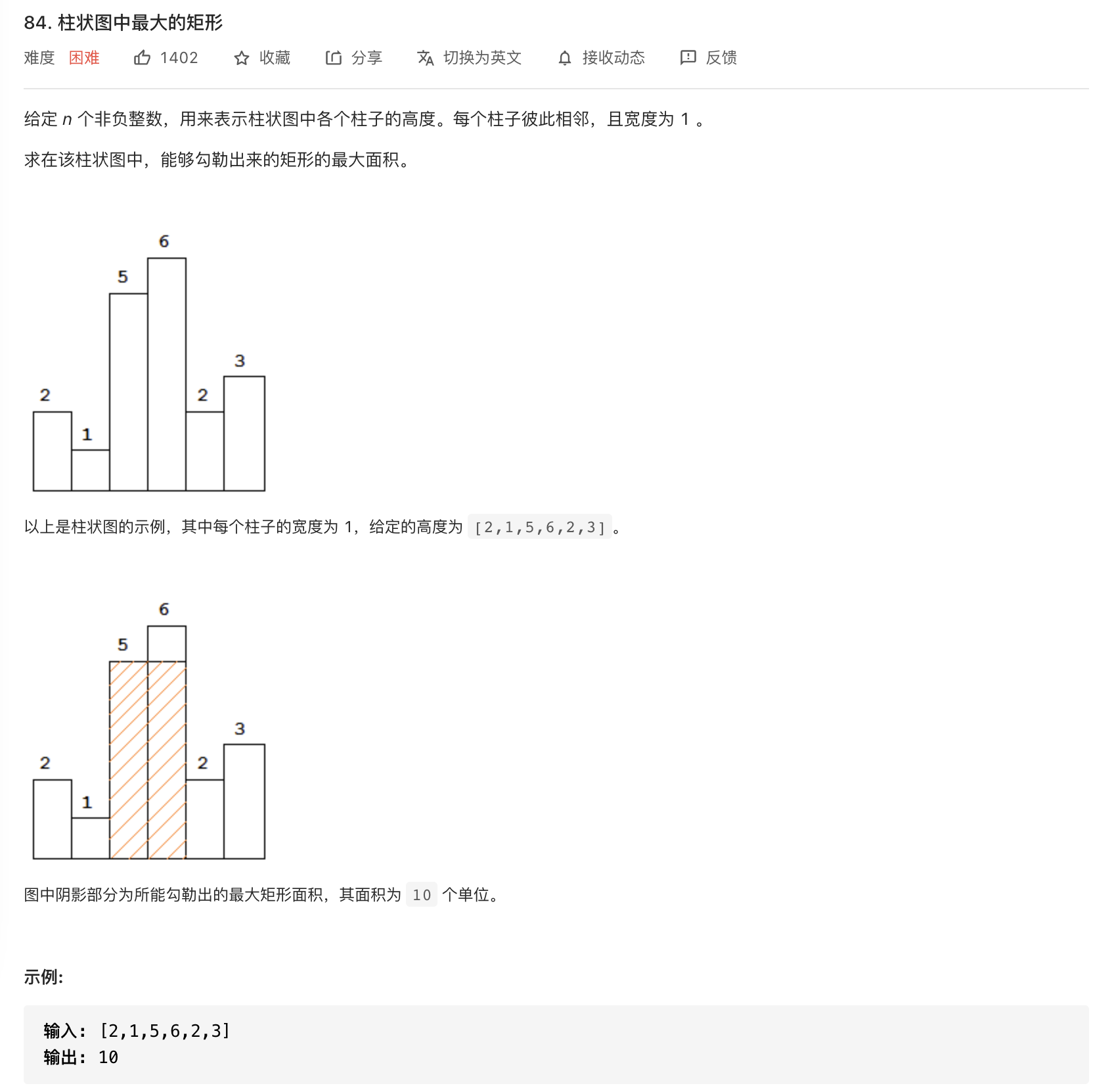
题目很容易读懂，计算能勾勒出的最大矩形面积，关键一点是能找到合适的高度和宽度，这就可以计算出最大面积，那么该如何计算找到合适的高度或者宽度呢？第一想法是遍历每一个柱子，决定该柱子能勾勒出多少的面积，关键在于找到它左右两边比它矮，且最靠近它的矩形的索引，这样就可以计算出每个矩形所横跨的宽度，那么就可以计算出每个矩形能勾勒出的面积，然后找到最大的就是最后的答案，这是一种暴力的解决办法，但是关键思想是正确的，就是找到矩形左右的边界，因为左右边界决定了能勾勒出的宽度。

暴力的方法如下代码所示：

/**
 * 暴力解法：O(n^2)，超出时间限制，固定高度，找到左右边界，它的边界是左右遇见的第一个比它矮的柱子
 *
 * @param heights 高度数组
 * @return 面积
 */
public int largestRectangleArea(int[] heights) {
    int area = 0;
    for (int i = 0; i < heights.length; i++) {
        int left = i;
        int right = i;
        int height = heights[i];
        while (left > 0 && heights[left - 1] >= height) {
            left--;
        }
        while (right < heights.length - 1 && heights[right + 1] >= height) {
            right++;
        }
        area = Math.max(height * (right - left + 1), area);
    }
    return area;
}

暴力方法简单直接，相信读者都能读懂，这里不再过多介绍，接下来，我们一起看下如何使用单调栈的方法来解决这道题。

首先我们明确的一点是，面积是由高度✖️宽度得出的，高度就是数组中每个元素的值，宽度其实就是数组中下标差-1。我们所做的还是需要找到某个柱子左右边界，也就是找到左右高度严格小于它的柱子，所谓严格小于，就是高度严格小于，如果是等于的话，也是无法确定它的边界的。

我们想想，这种场景是否是可以构造单调递增栈？单调递增栈，越往栈底，值越小，在遍历数组的过程中，如果遇见某个元素小于当前栈顶元素，那么这就不找到栈顶元素的右边界了？因为是单调递增栈，所以栈顶元素的左边界是一定在栈内的，这样就可以计算出栈顶元素能勾勒出的面积。另外一点值得注意，因为柱子的高度我们是可以通过下标来直接获取的，所以在栈中不是记录柱子的高度，而是记录柱子的索引下标。

我们接下来使用题目中的案例，画图来描述这一过程，方便大家理解。题目中的柱子高度数组是[2, 1, 5, 6, 2, 3]，图解过程如下：

• 第一步：遍历下标0的位置，此时还无法确定高度为2能构造出的最大面积，此时0下标直接入栈；
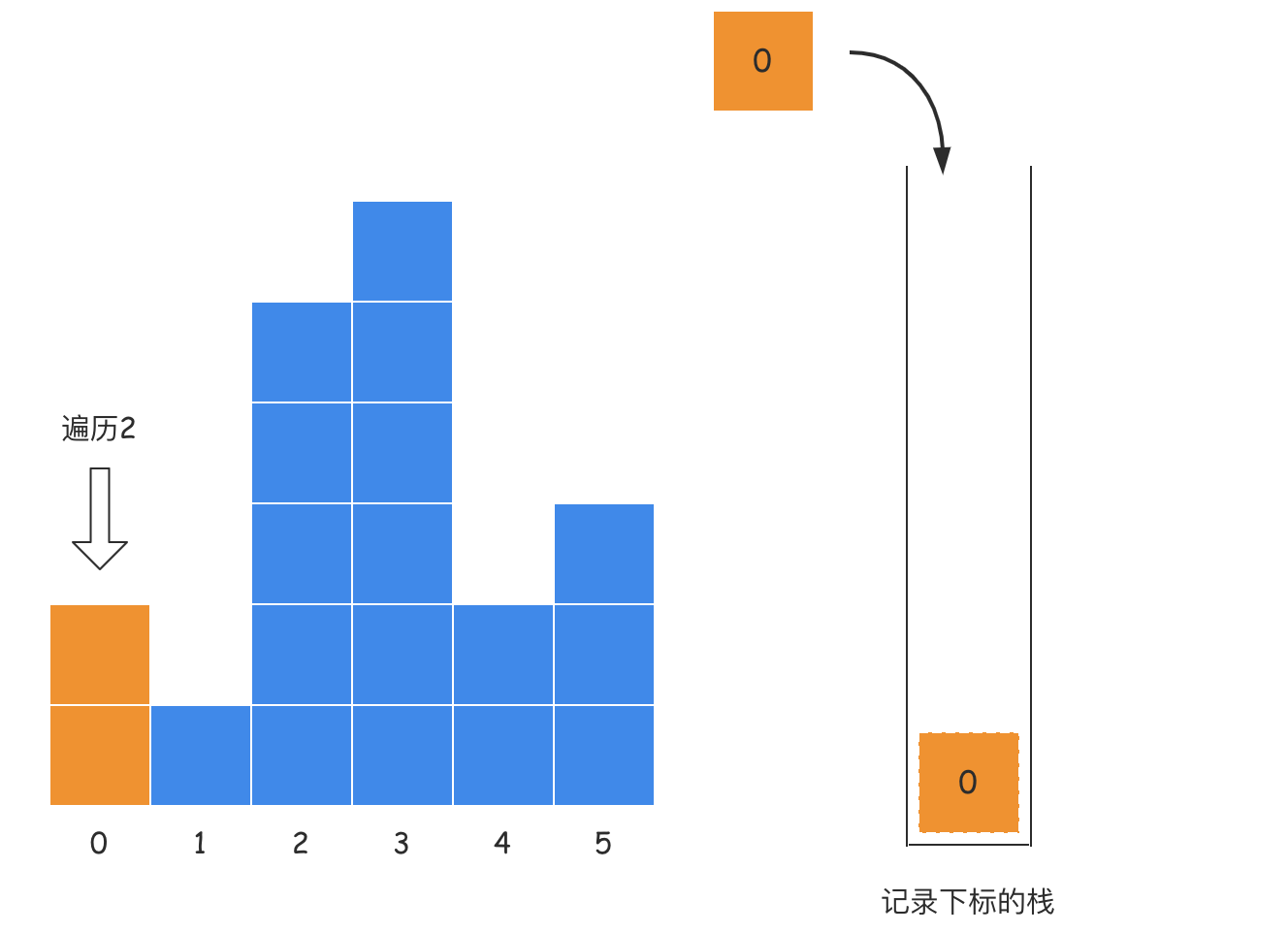
• 第二步：遍历下标1的位置，此时栈顶记录的索引为0，0对应的高度为2，大于下标1对应的高度1，所以此时栈顶0的左边界是-1，右边界是1，所以宽度为1，即1 - (-1) - 1，这个时候就可以确定栈顶索引0对应高度所能构造出的最大面积为2，此时弹出栈顶元素0，索引1入栈；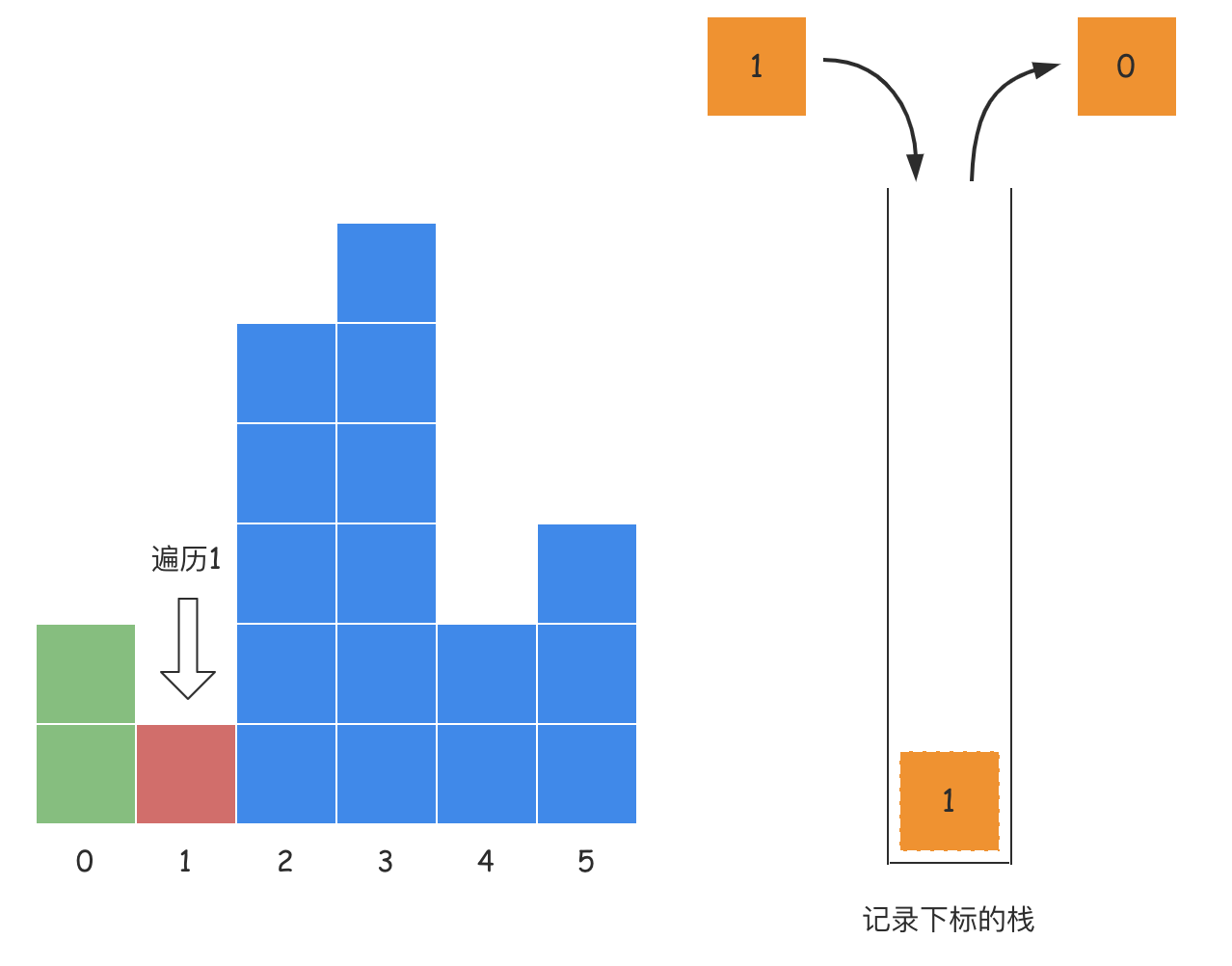
• 第三步：遍历下标2的位置，索引2对应的高度为5，大于当前栈顶元素对应的高度1，直接入栈；
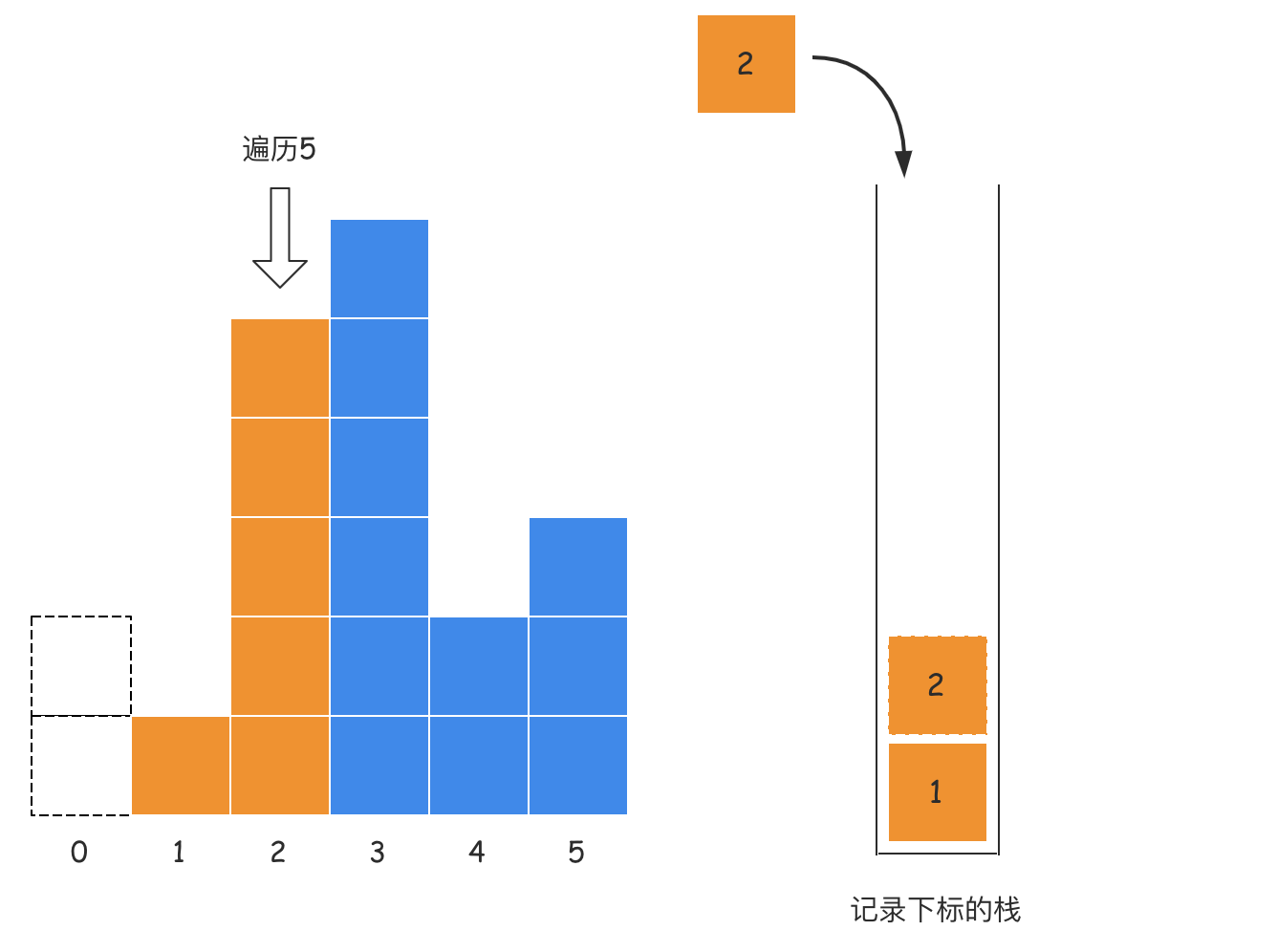
• 第四步：遍历下标3的位置，索引3对应的高度6大于当前栈顶对应的高度5，直接入栈；
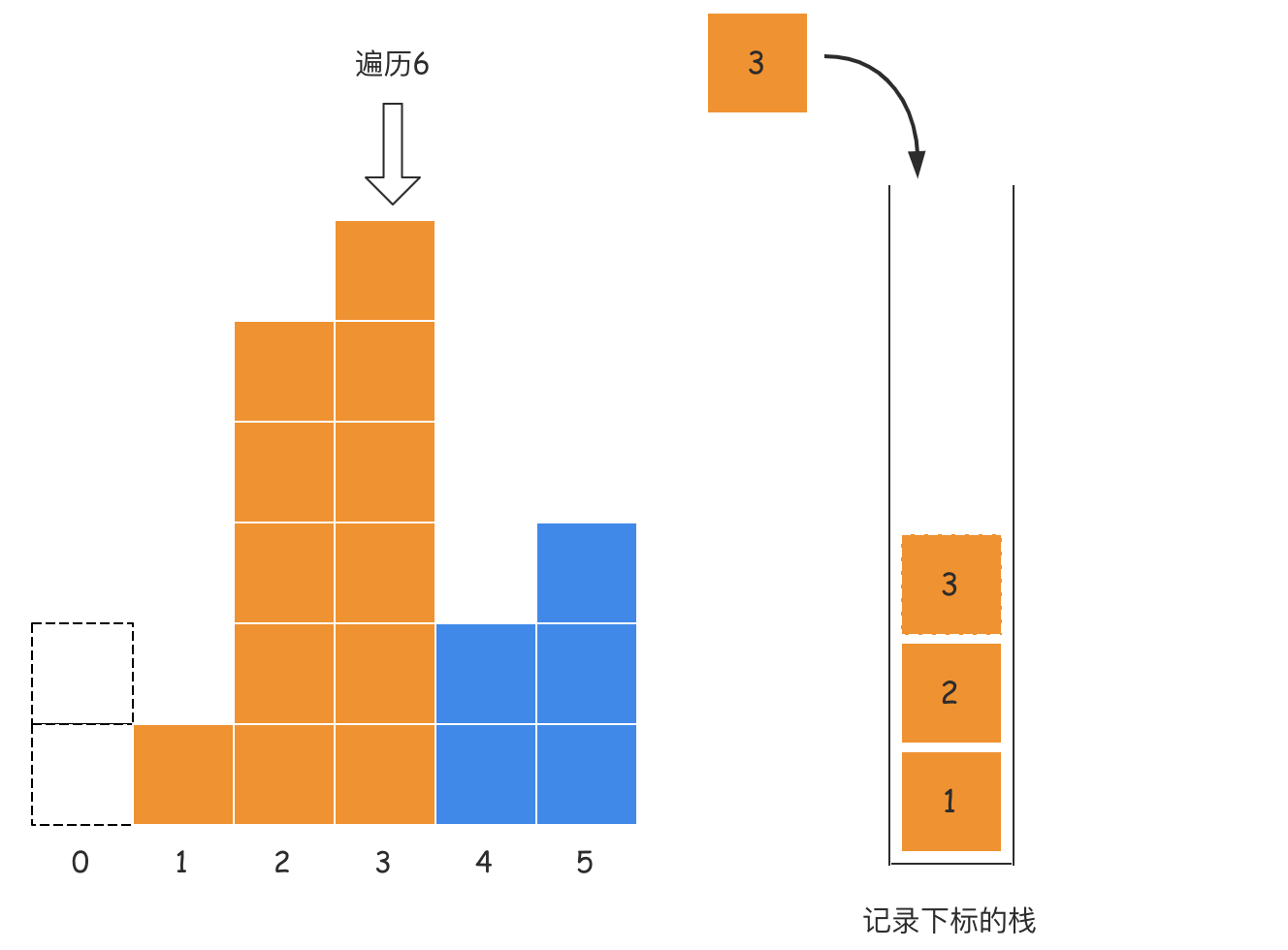
• 第五步：遍历下标为4的位置，发现栈顶元素3对应的高度为6，大于当前下标4对应的高度2，所以此时就找到了栈顶元素4对应的高度6的右边界，栈顶元素4对应的左边界就是它弹出后的栈顶元素2，所以宽度为1，即4 - 2 - 1，此时计算出的高度为6的柱子构造出的最大面积就是6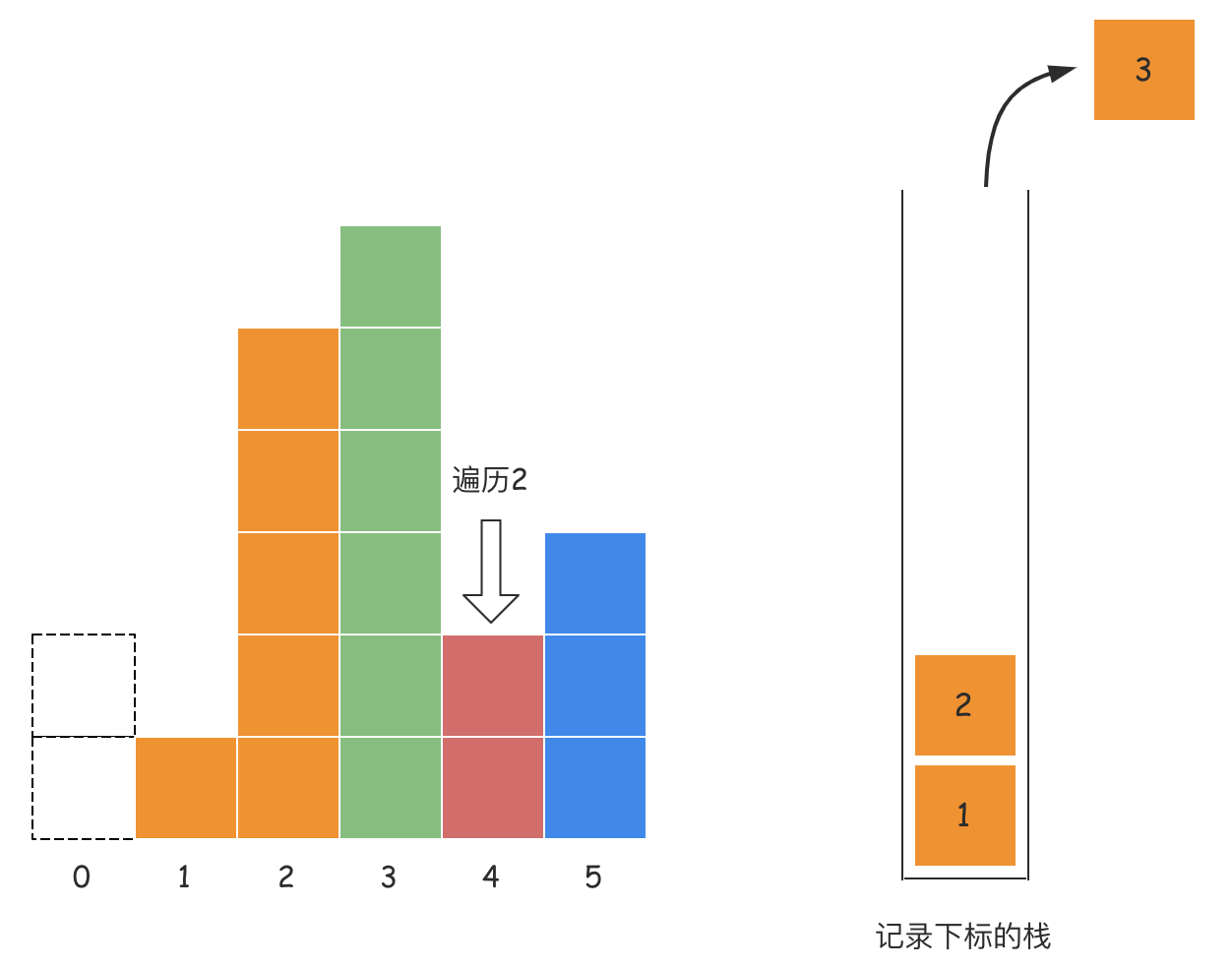； 当3弹出后，计算出了3对应的高度6的构造出来的面积为6，此时栈顶元素为2，它所对应的高度5仍然大于索引4对应的高度2，所以高度5的左边界索引为1，右边界索引为4，所以宽度为2，即4 - 1 -1，所以高度5构造出来的最大面积是10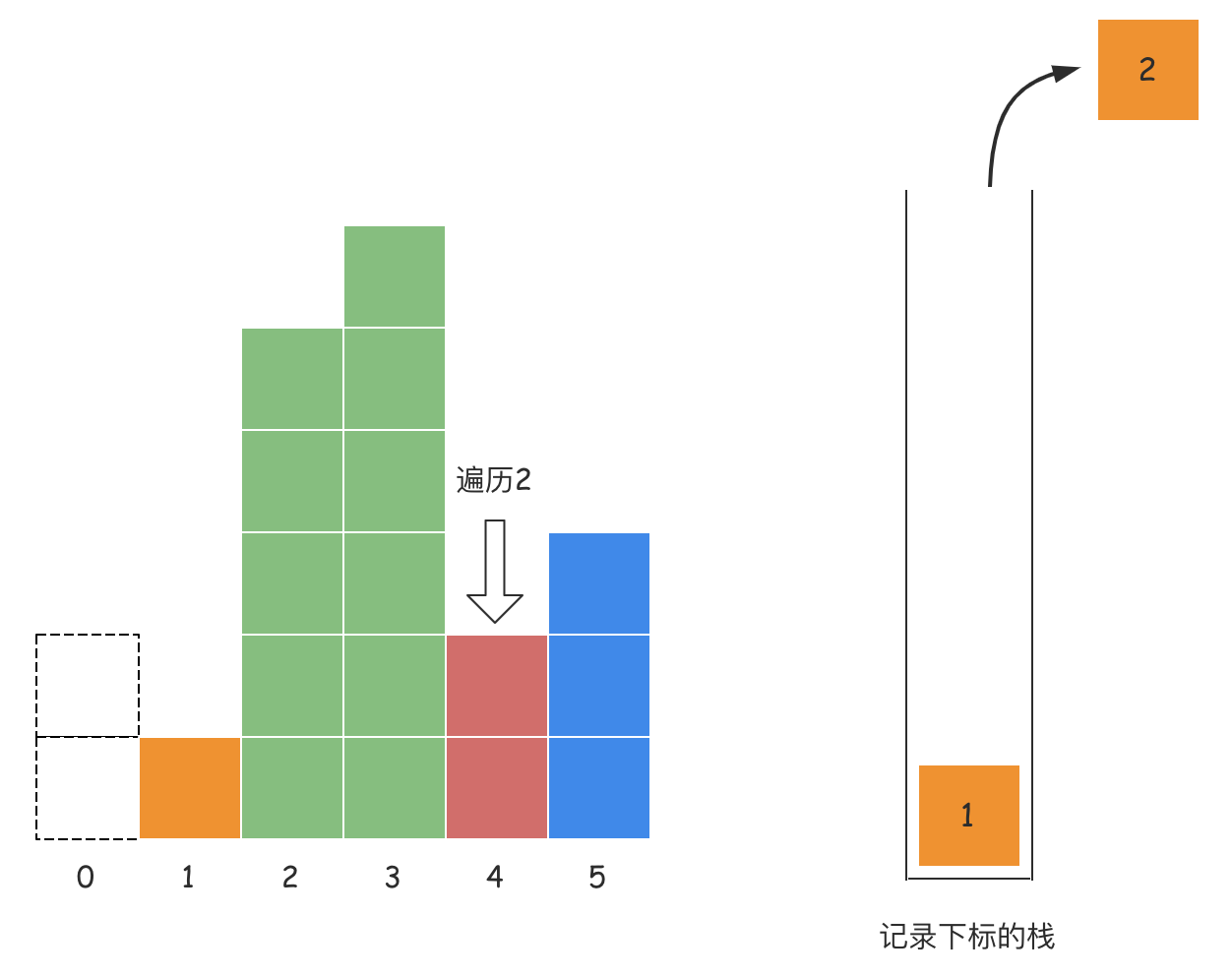； 当2弹出后，栈顶元素为1，此时栈顶元素1对应的高度1是小于4对应的高度2的，所以此时4入栈，到这里。下标2和3对应的高度构造出的面积都已经算出来了，分别是10和6；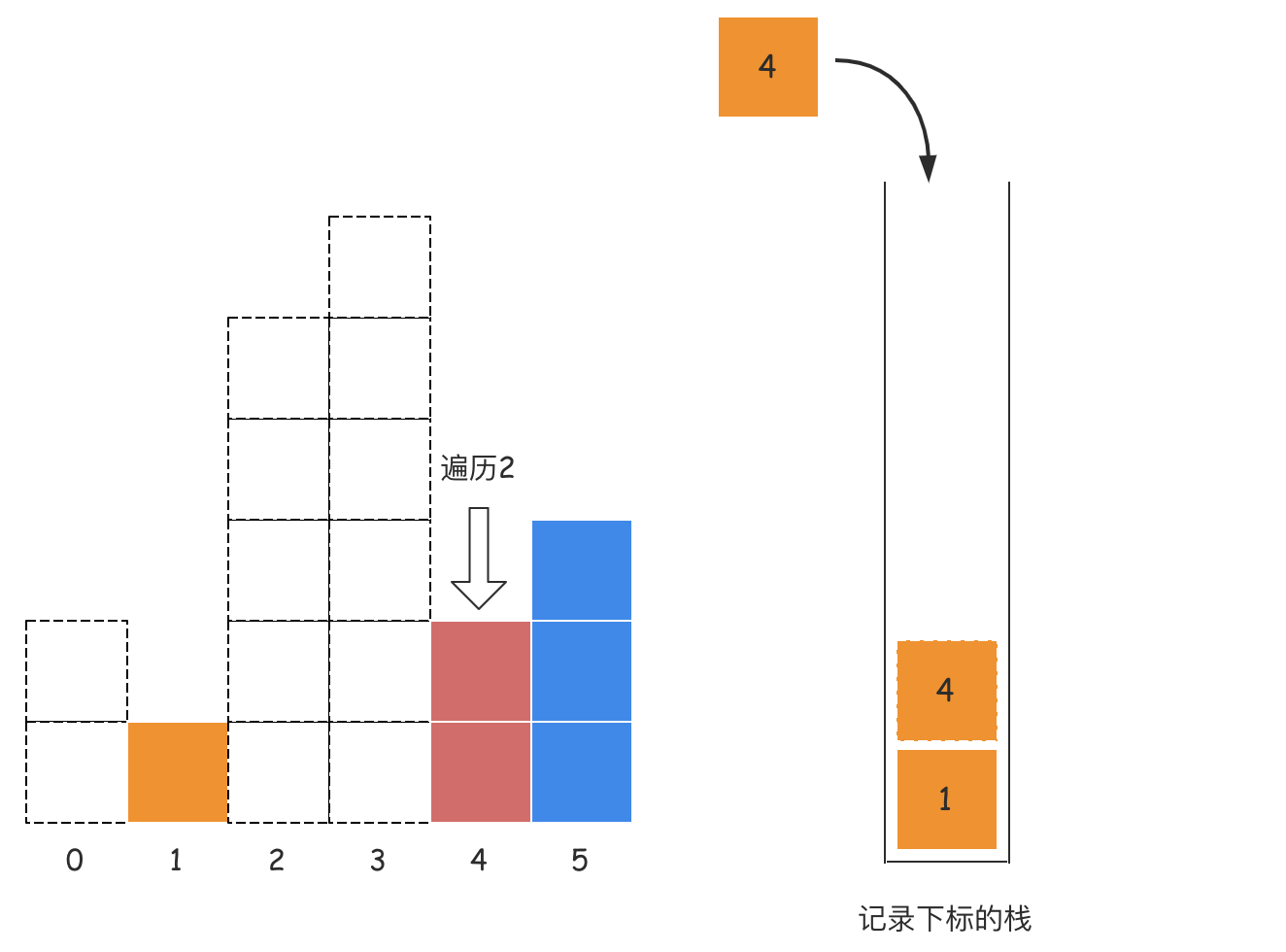
• 第六步：遍历下标为5的位置，此时下标5的对应的高度3是大于栈顶元素4对应的高度2的，所以直接入栈，此时遍历结束，栈内的元素从栈底到栈顶分别是1，4，5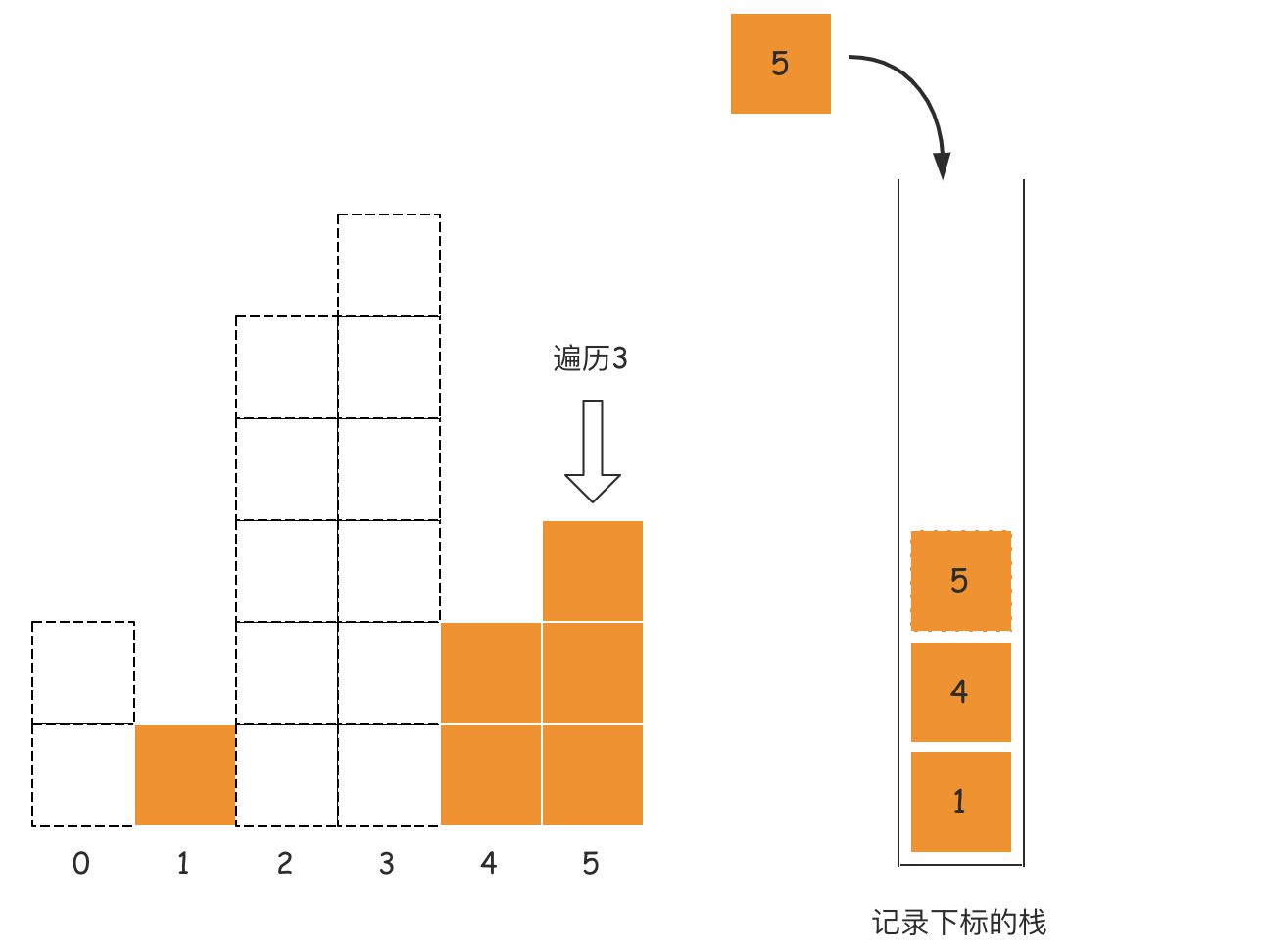； 有读者读到这里，肯定有疑问，接下来该如何处理剩下的三个高度所能构造出的最大面积？其实可以加一个判断，如果遍历的元素到了数组末尾，我们可以假设还有一个元素，索引位置为6，高度为0，为什么可以这么假设？因为数组的所有元素都是非负整数，那么0肯定是最小的，也就是没有高度的，如下图所示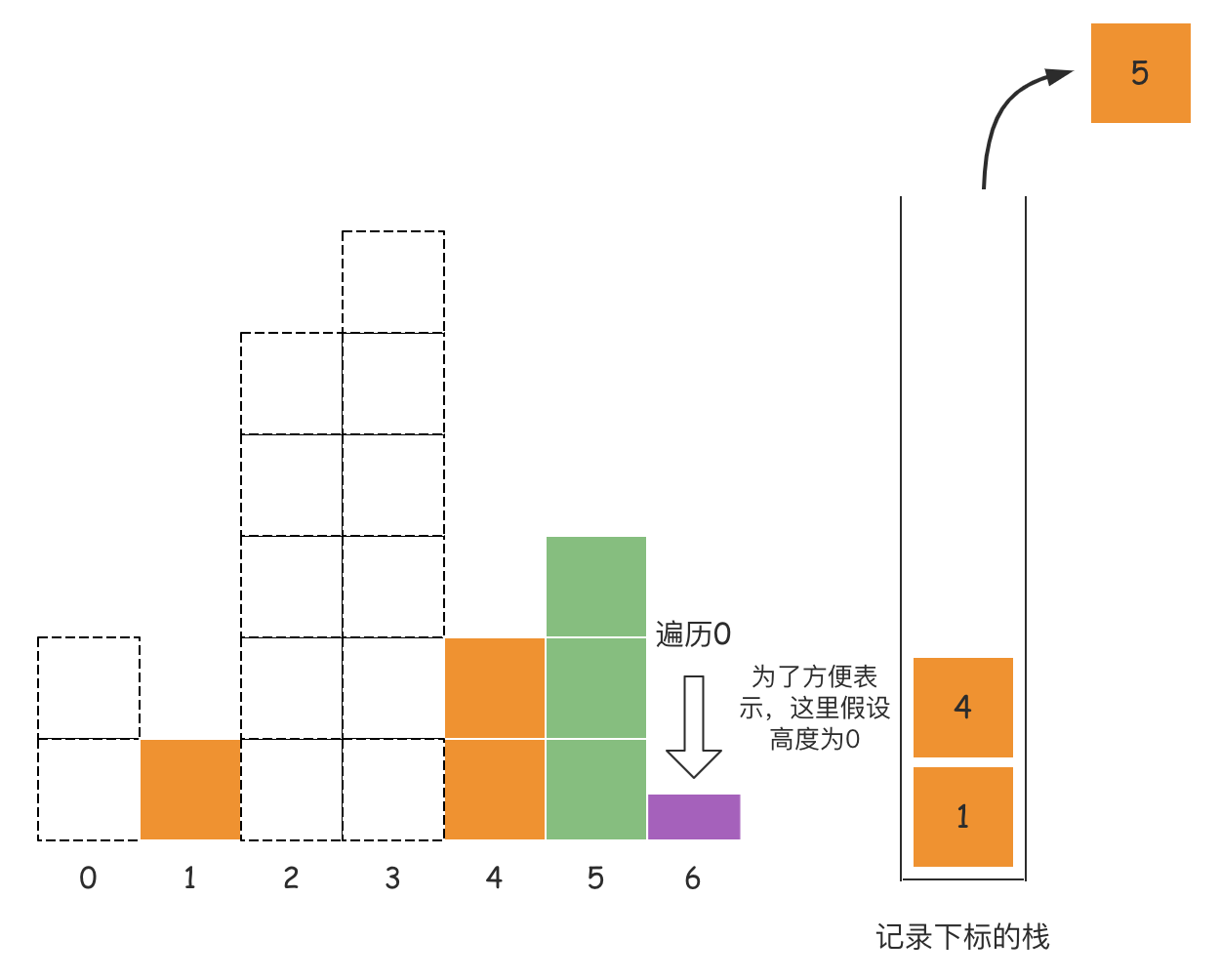： 此时计算出索引5多对应的高度3所构造出来的面积是3，因为宽度是1，即6 - 4 -1；同理栈顶元素4对应的右边界是6，左边界是1，所以索引4对应的高度2构造出来的面积是8，因为宽度是4，即6 - 1 - 1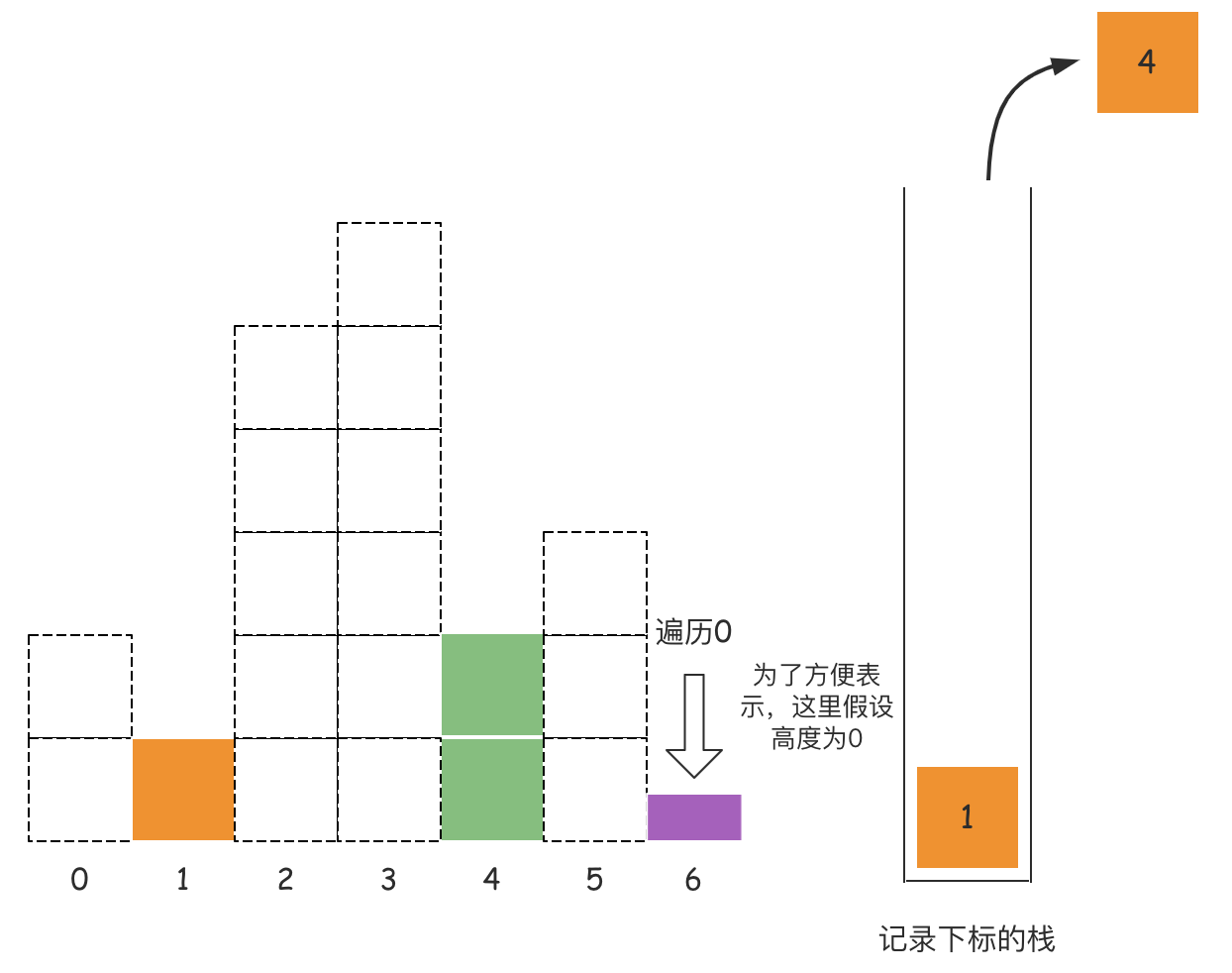； 那么该如何计算出最后一个1索引对应的面积呢？其实可以假设在数组的最左边有个下标为-1，高度为0的柱子，那么索引为1对应的高度左边界是下标-1，右边界是6，所以宽度是6，即6 - (-1) - 1，这就把所有的高度所能构造出来的面积都计算了，找到最大的即可。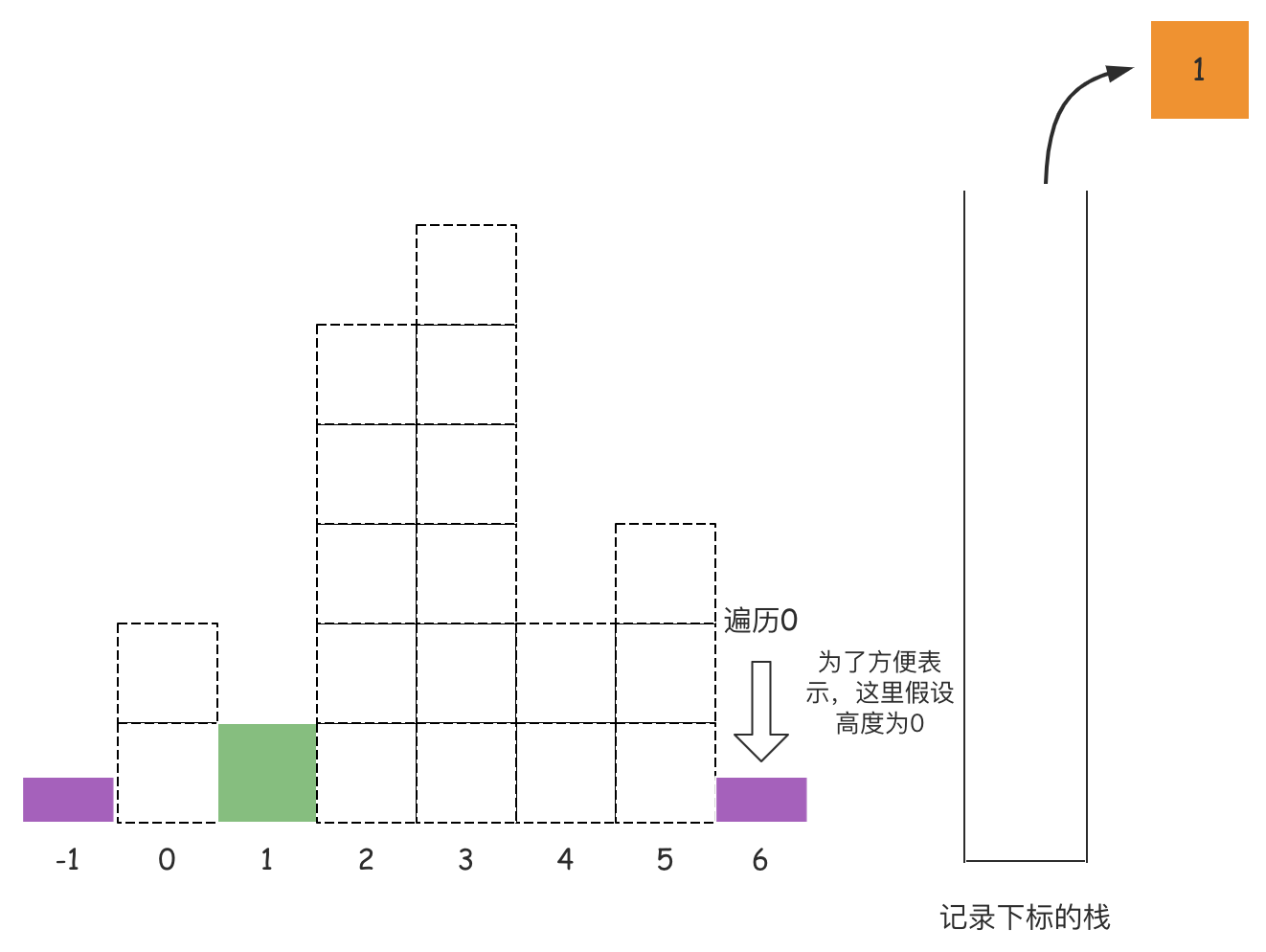 有了这么丰富的图来配合分析，是不是要清晰很多？需要说明一点的是，最后谈到的假设高度为0的柱子加入到数组两端，其实这是一种常见的思想——哨兵，在数组两端加入哨兵来辅助解决问题，这种思想需要读者好好体会，leetcode中有许多题目都使用到了这种思想。

解析到这里，读者应该可以写出解决问题的代码了，这里直接贴出代码，如下所示：

/**
 * 单调栈+哨兵解法：O(n)
 *
 * @param heights 高度数组
 * @return 最大面积
 */
public int largestRectangleArea(int[] heights) {
    if (heights.length == 0) {
        return 0;
    }
    if (heights.length == 1) {
        return heights[0];
    }
    // 面积
    int area = 0;
    // 添加哨兵:数组两端各加上一个为0的元素
    int[] newHeights = new int[heights.length + 2];
    System.arraycopy(heights, 0, newHeights, 1, heights.length);
    newHeights[0] = 0;
    newHeights[heights.length + 1] = 0;
    heights = newHeights;

    // 单调栈
    Stack<Integer> stack = new Stack<>();
    // 加入哨兵，stack中就无需做非空判断，因为0索引对应的高度为0，肯定是数组中最小的
    stack.push(0);
    for (int i = 1; i < heights.length; i++) {
        while (heights[i] < heights[stack.peek()]) {
            int currentHeight = heights[stack.pop()];
            int currentWight = i - stack.peek() - 1;
            area = Math.max(area, currentHeight * currentWight);
        }
        stack.push(i);
    }
    return area;
}

代码是不是很简答？单调栈的解题思路很有效，希望读者好好体会。

3.8 接雨水 困难

经过上面7道题的练习，看到leetcode第42题：接雨水，那么我想你很快就会想到使用单调栈来解决这个问题。这道题是一道困难题，但是如果你的单调栈思想融会贯通了，我个人觉得这道题只能算一道中等题。

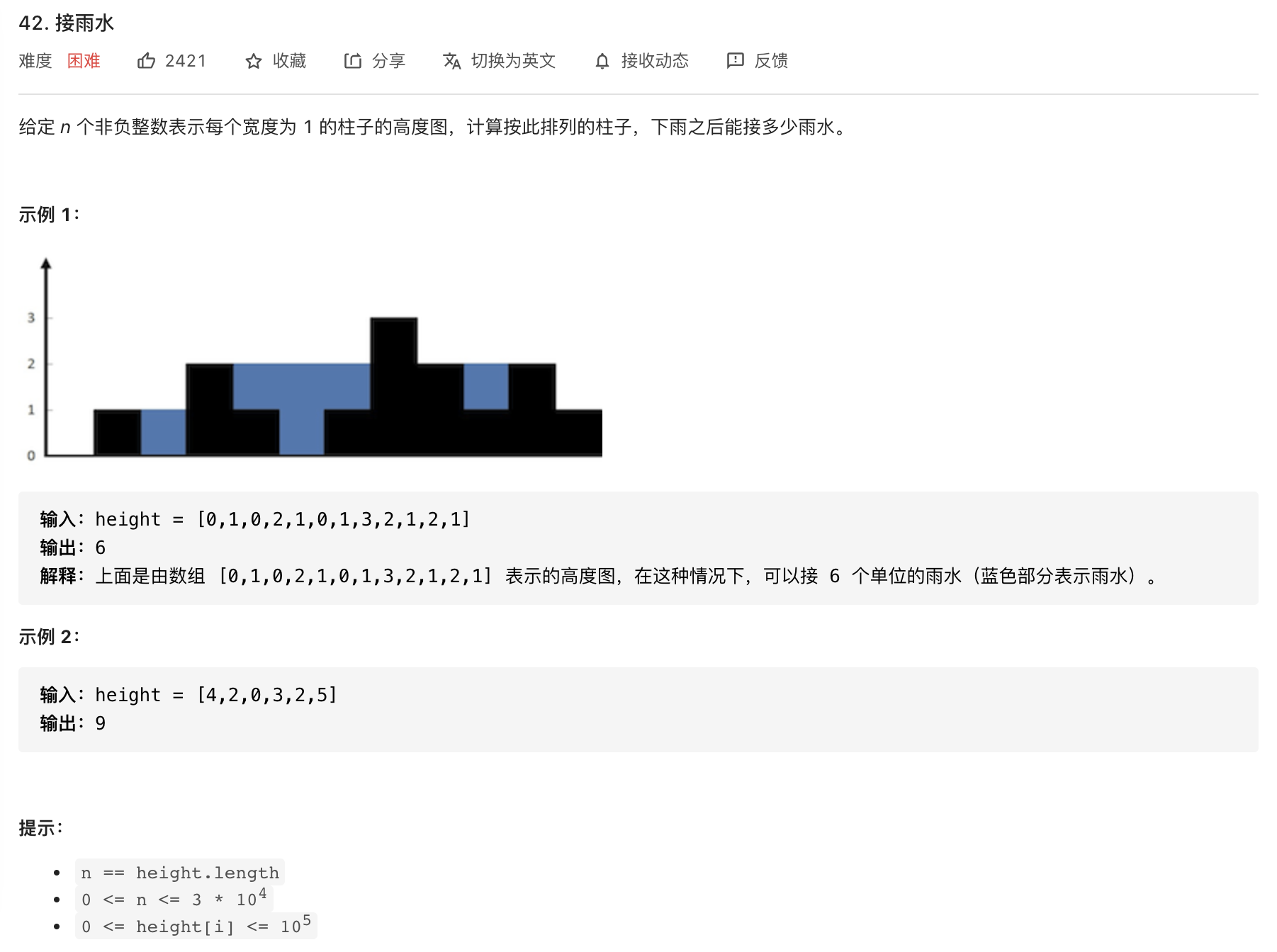
我们做个简单分析：从左向右遍历数组，且维护一个单调递减栈，栈内存储的是数组的下标索引。当遍历的元素小于等于栈顶索引对应的元素的时候，这个被遍历的元素下标直接入栈；当出现某个元素大于栈顶下标对应的元素的时候，这个时候说明左右边界可能已经围出了一个凹地，那么这个凹地可以承接雨水的，那么就需要计算承接雨水的面积。

这里从数组的角度来看这个问题：维护一个单调栈，单调栈存储的是数组元素的下标，满足从栈底到栈顶的下标对应的数组中的元素递减（非严格）。

从左到右遍历数组，遍历到下标i时，如果栈内至少有两个下标，记栈顶的数值为peek，那么peek的下面一个值记为left，则一定存在关系：height[peek] >= height[left]（单调栈特点）。如果满足height[i] > height[peek]，则得到一个可以接雨水的凹地，该凹地的宽度是i - left - 1，高度是Math.min(height[left], height[i]) - height[peek]，则凹地面积，也就是可以接水的面积可以根据这个宽度和高度进行计算得到。

在这个过程中，为了得到left，需要将peek出栈。在对peek计算能接的雨水量之后，left变成新的 peek，重复上述操作，直到栈变为空，或者遍历结束后栈顶下标对应的数组元素大于或等于height[i]。

在对下标i处计算能接的雨水量之后，将i入栈，继续遍历后面的下标，计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。

如果上述的文字分析没有理解，那么可以看下面的图：

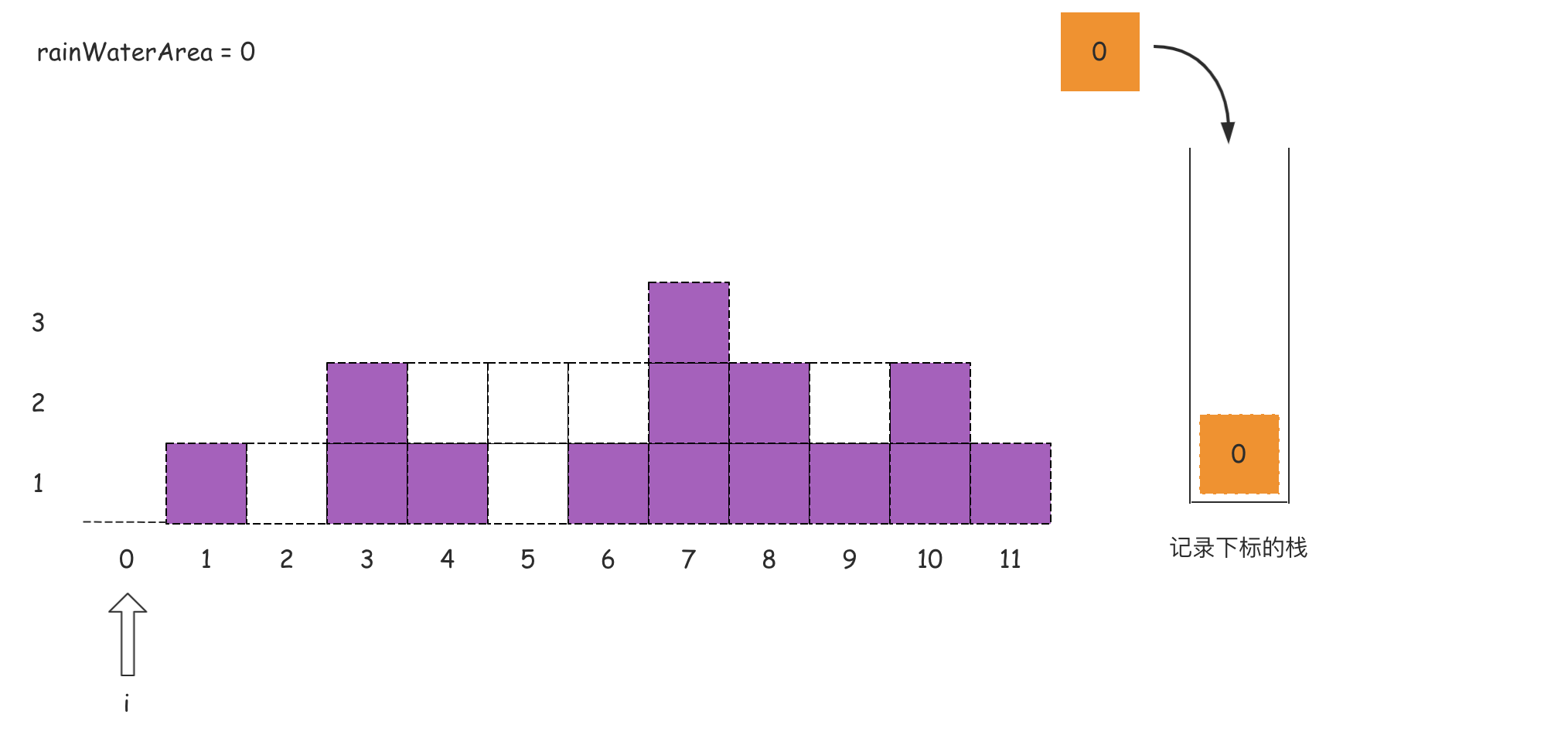
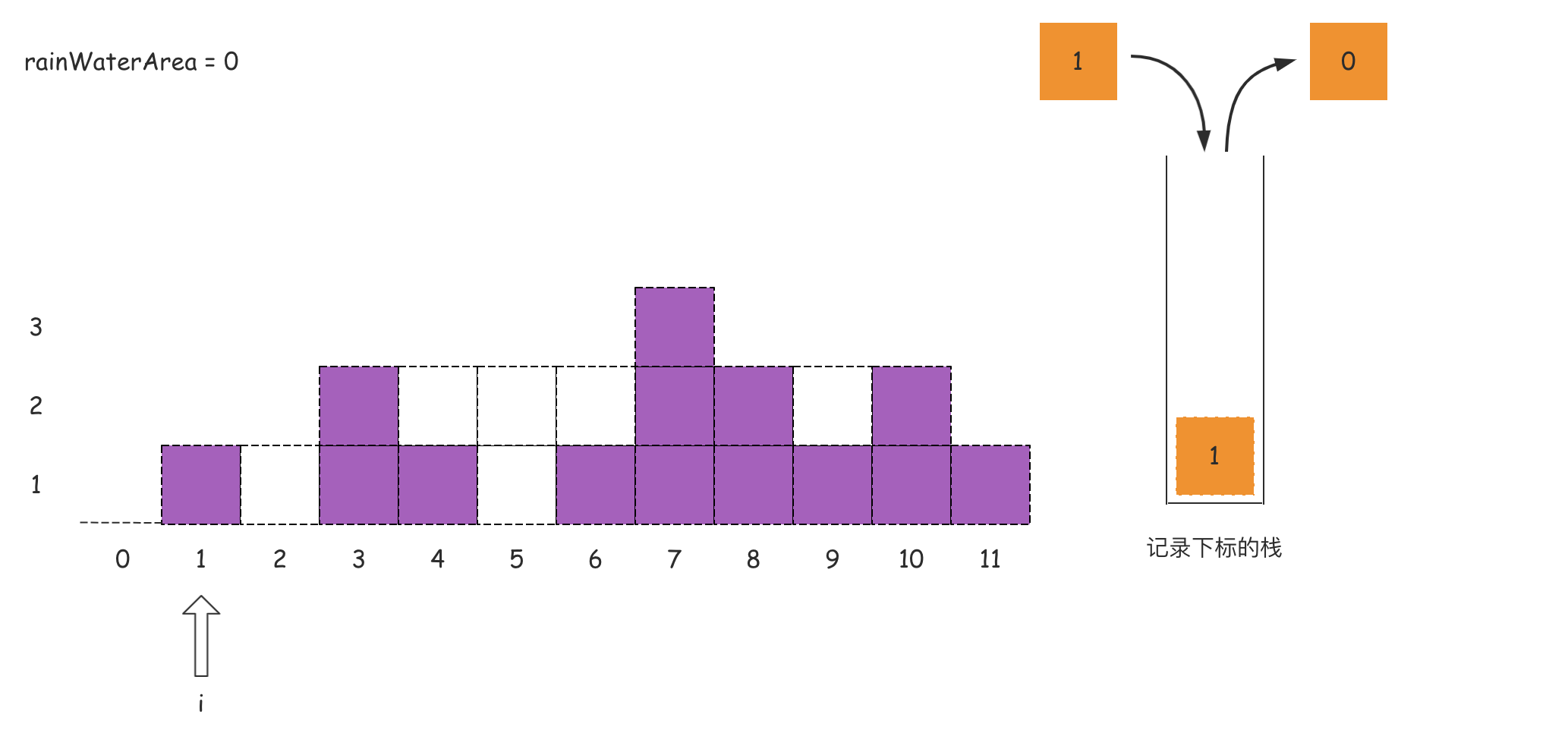
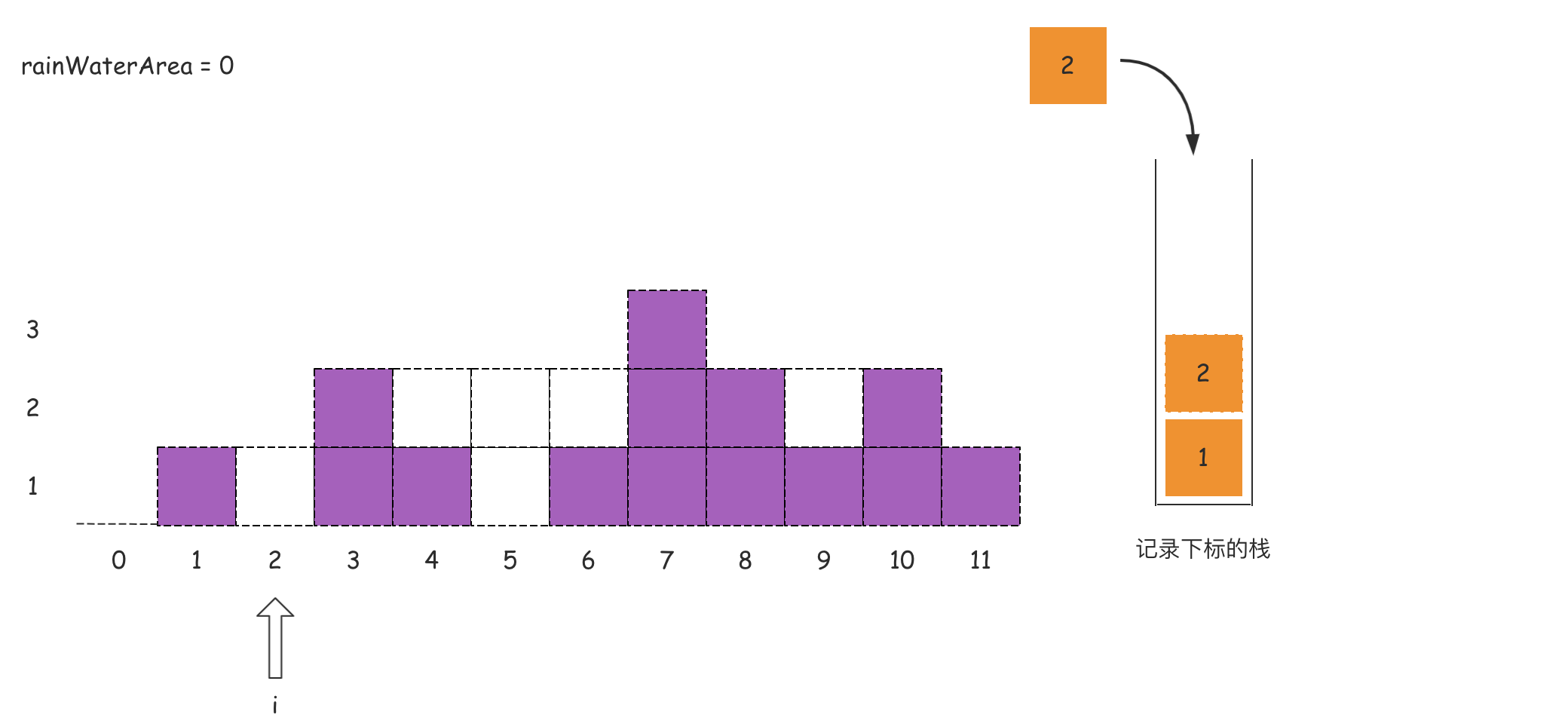
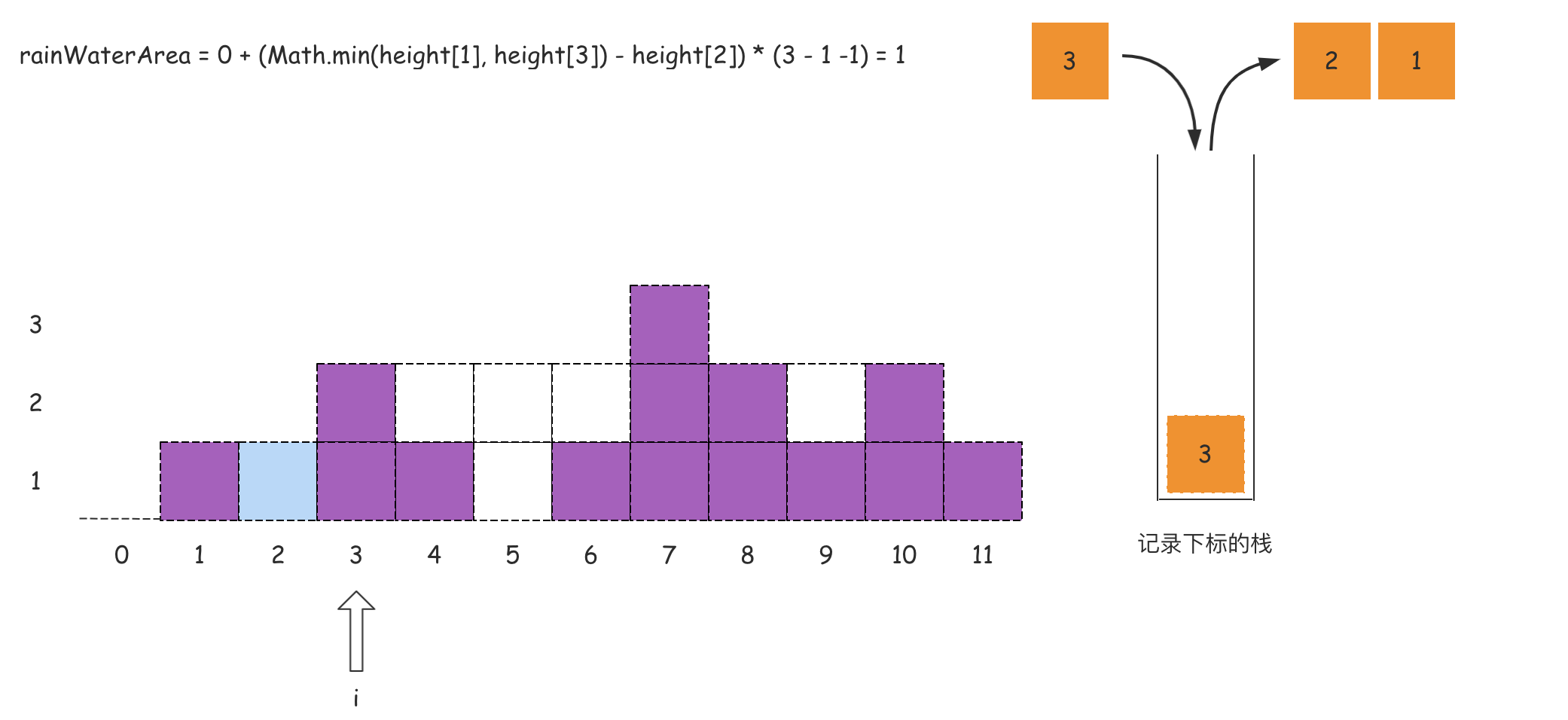
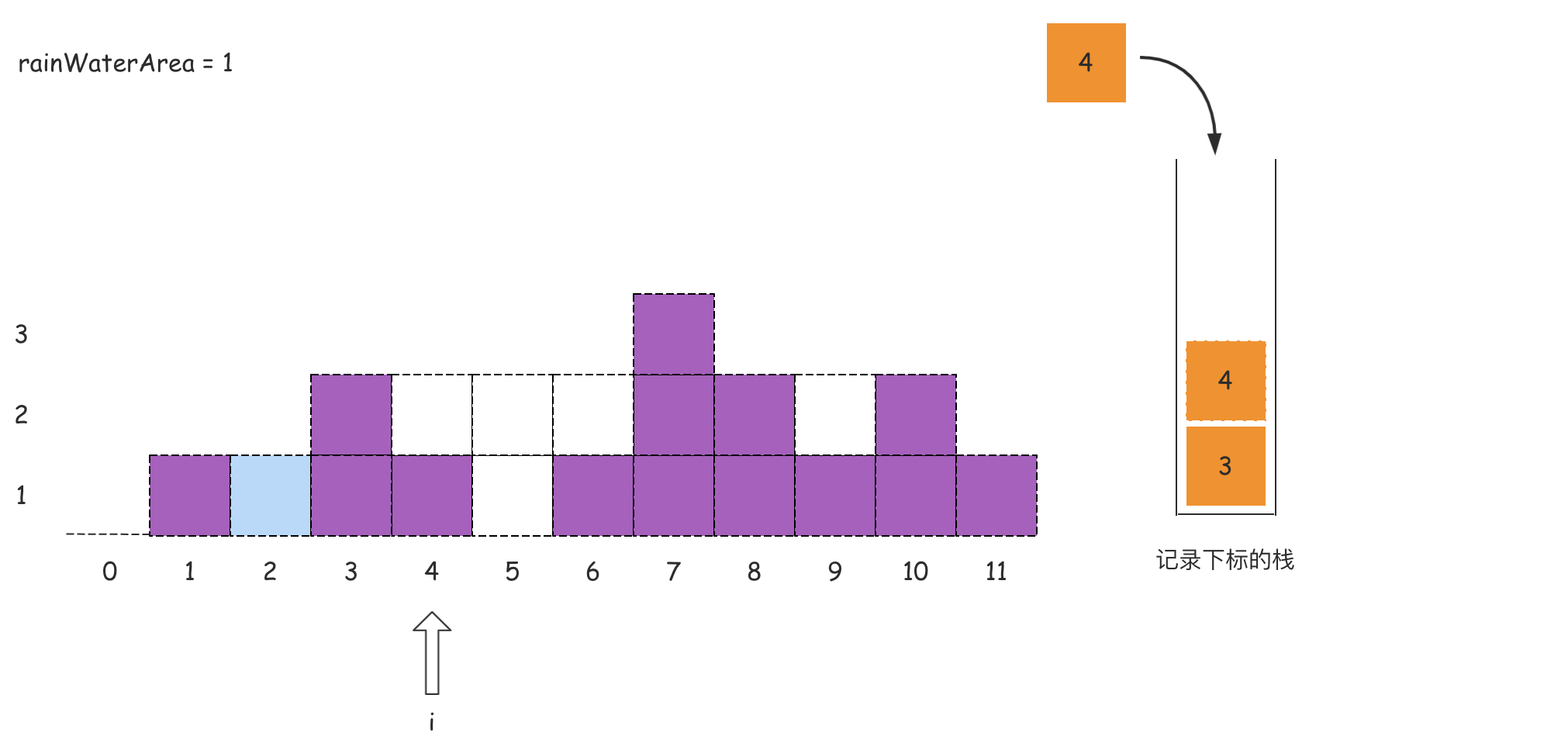
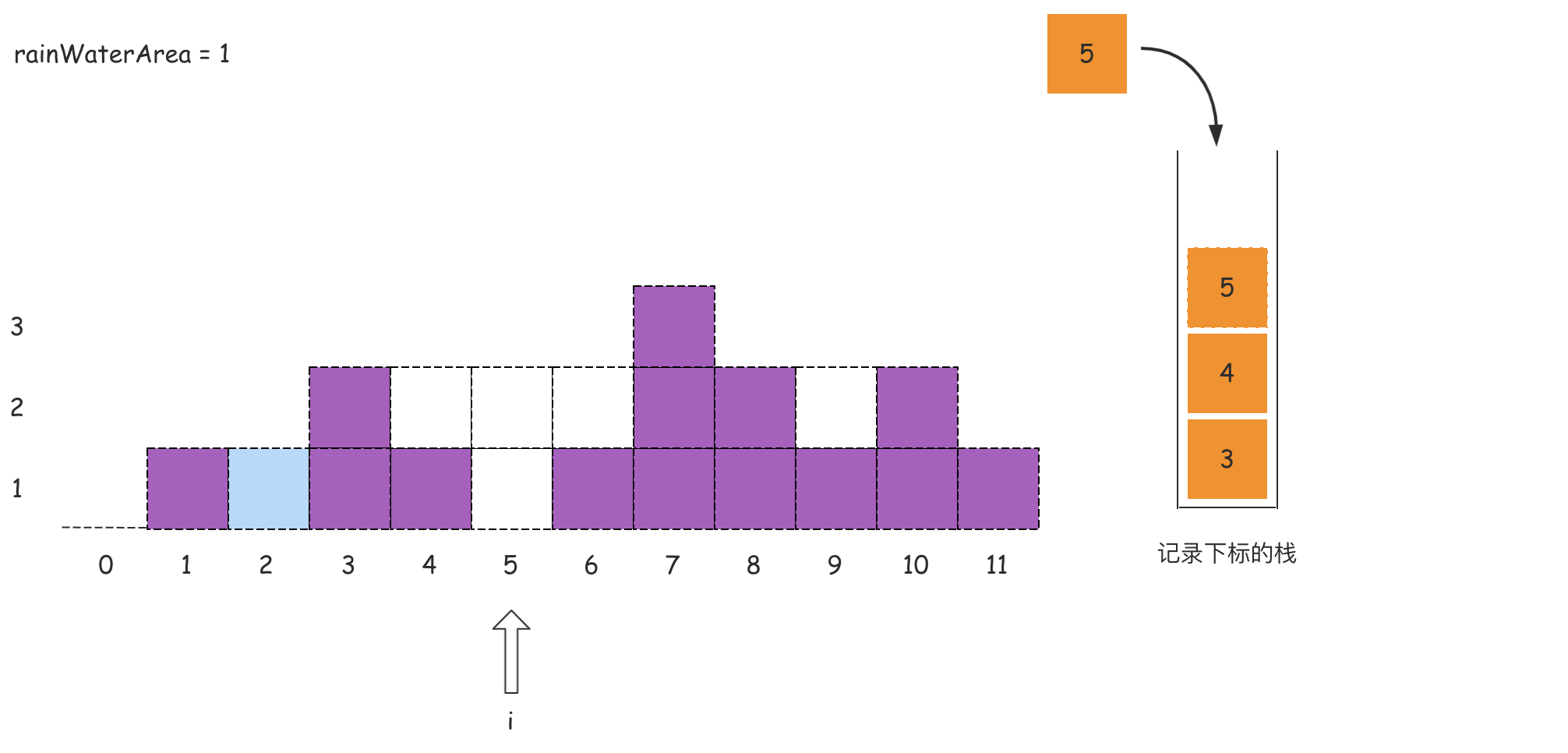
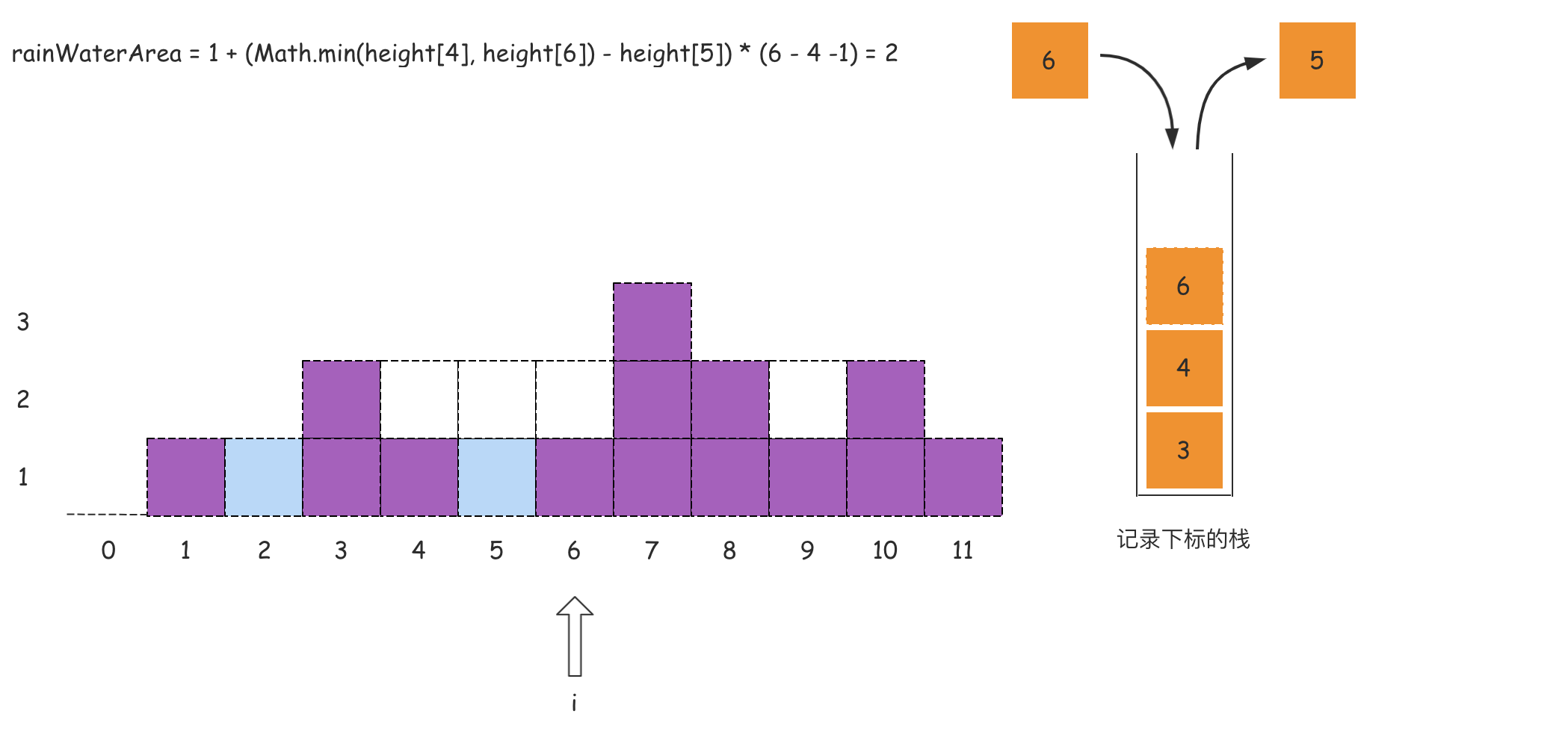
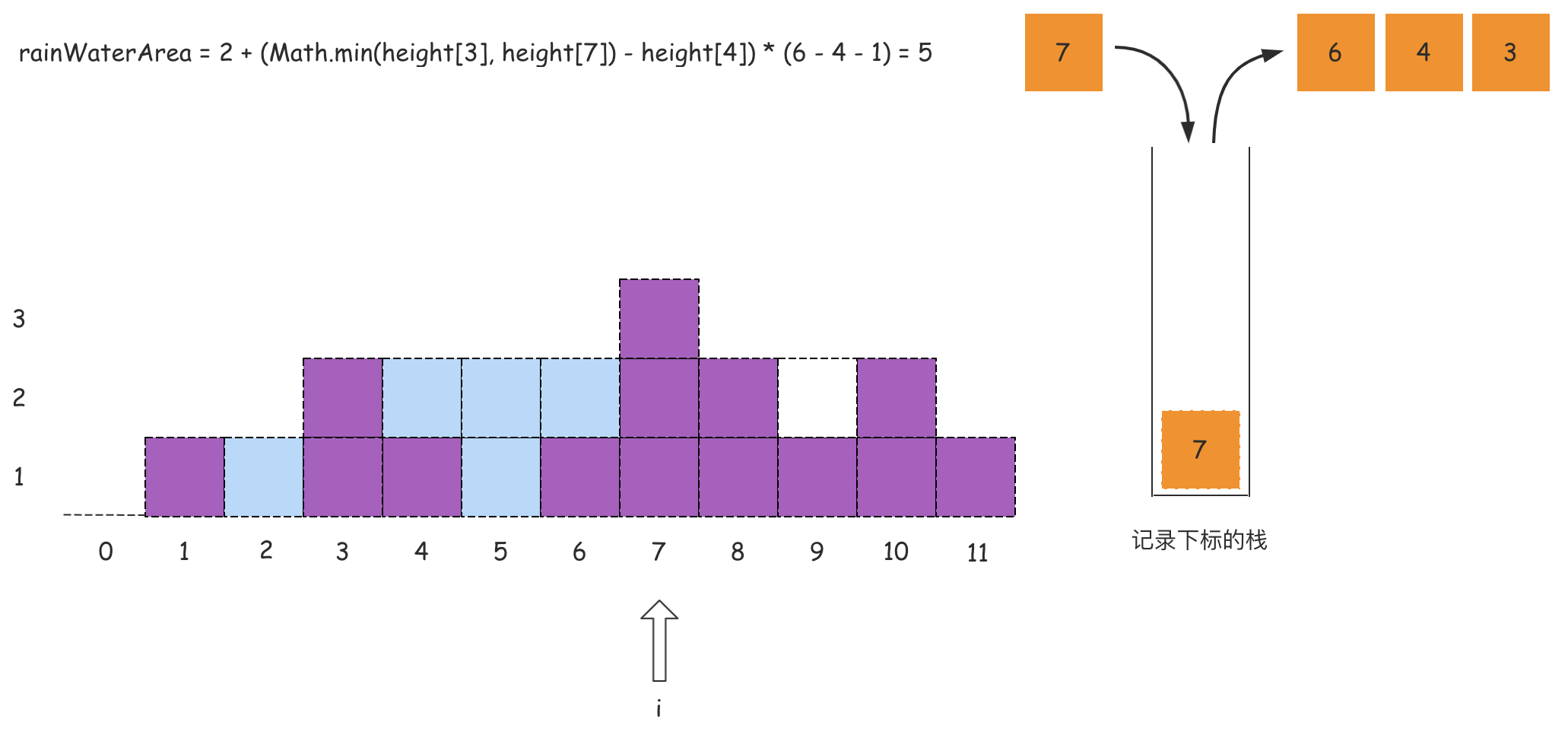
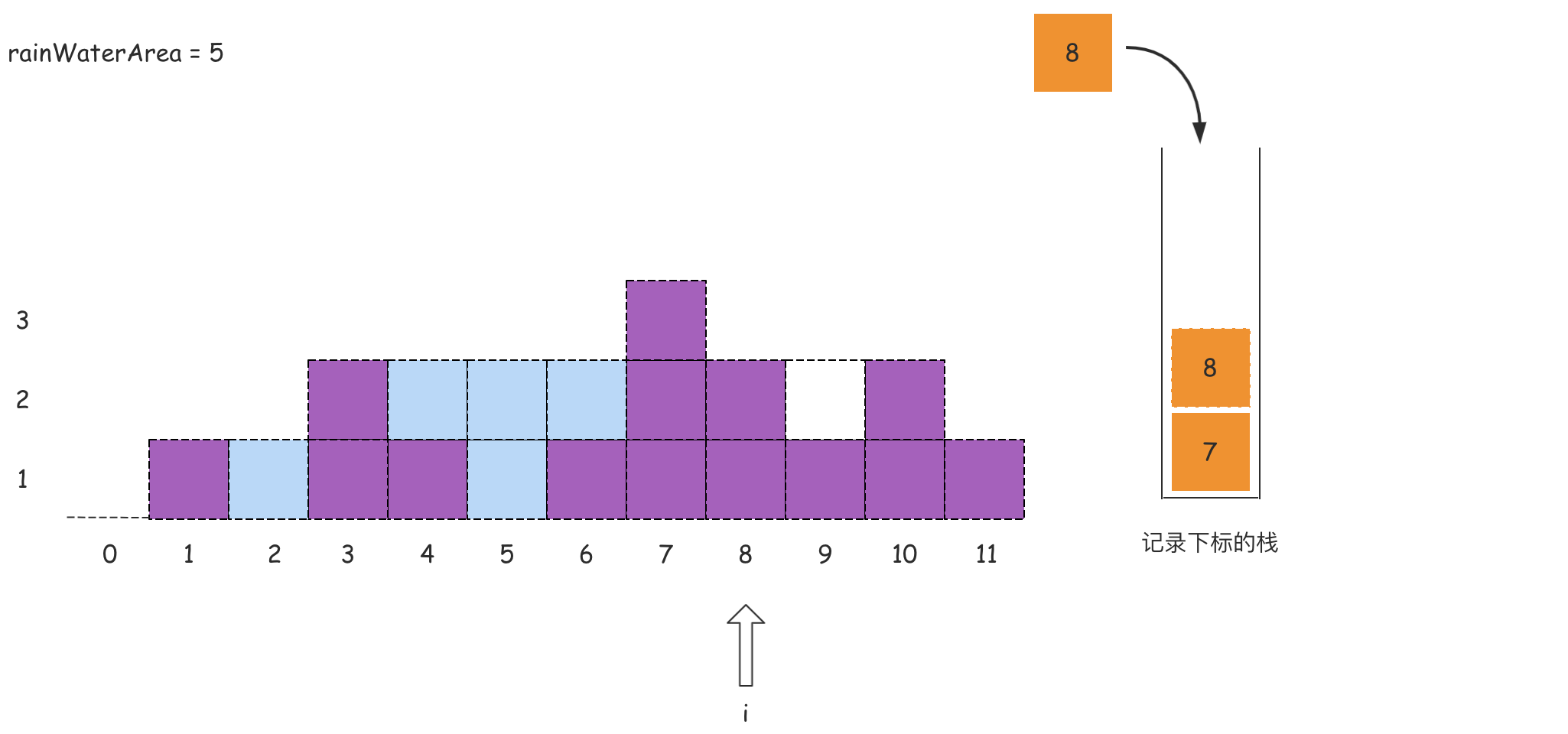
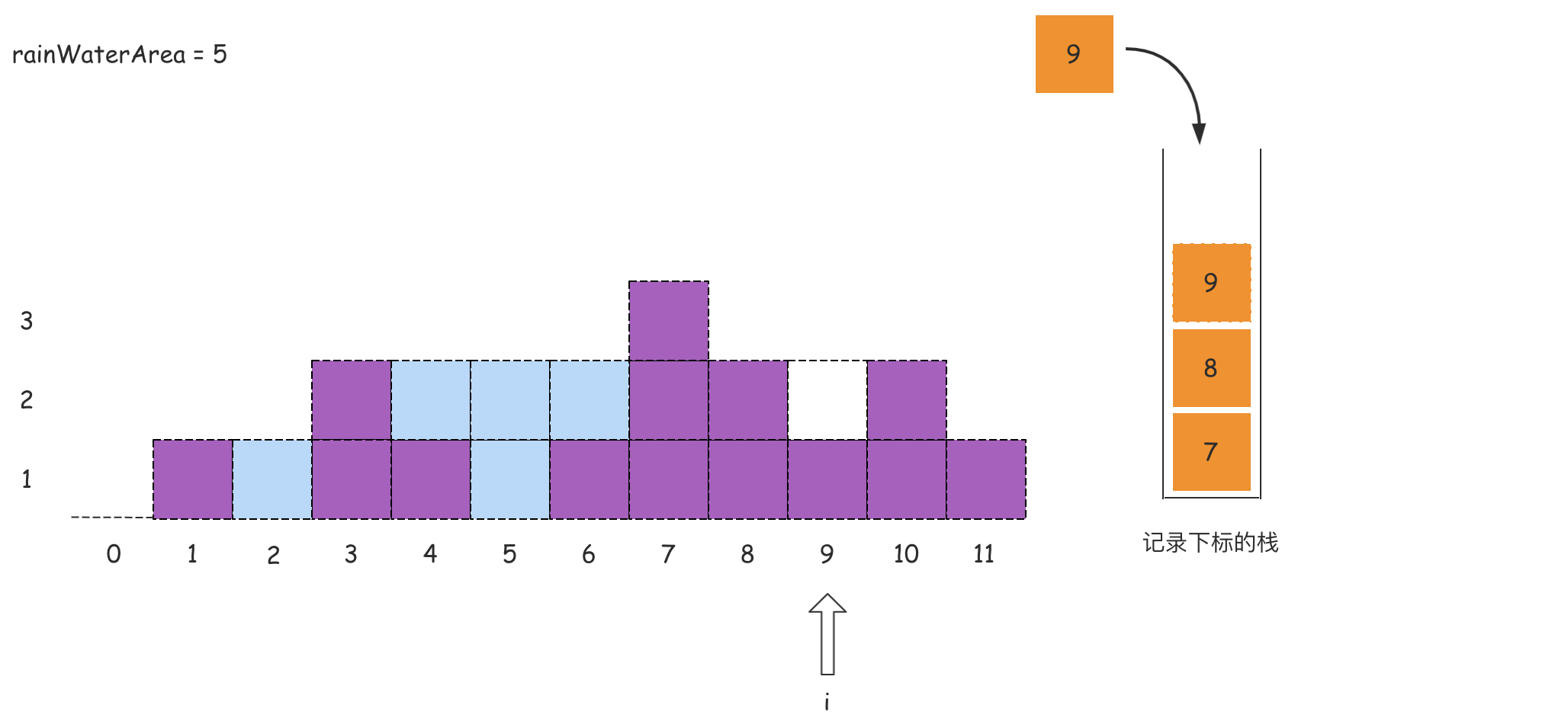
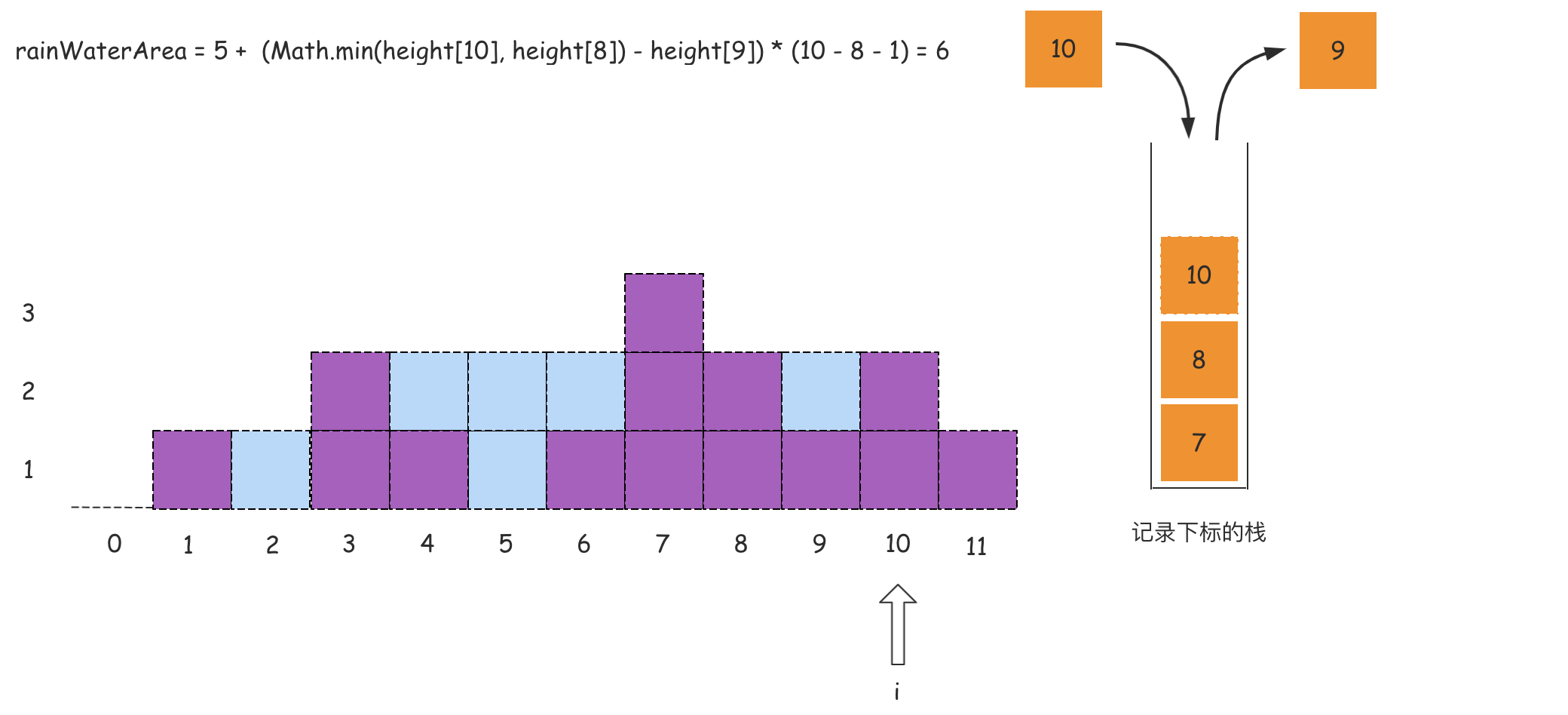
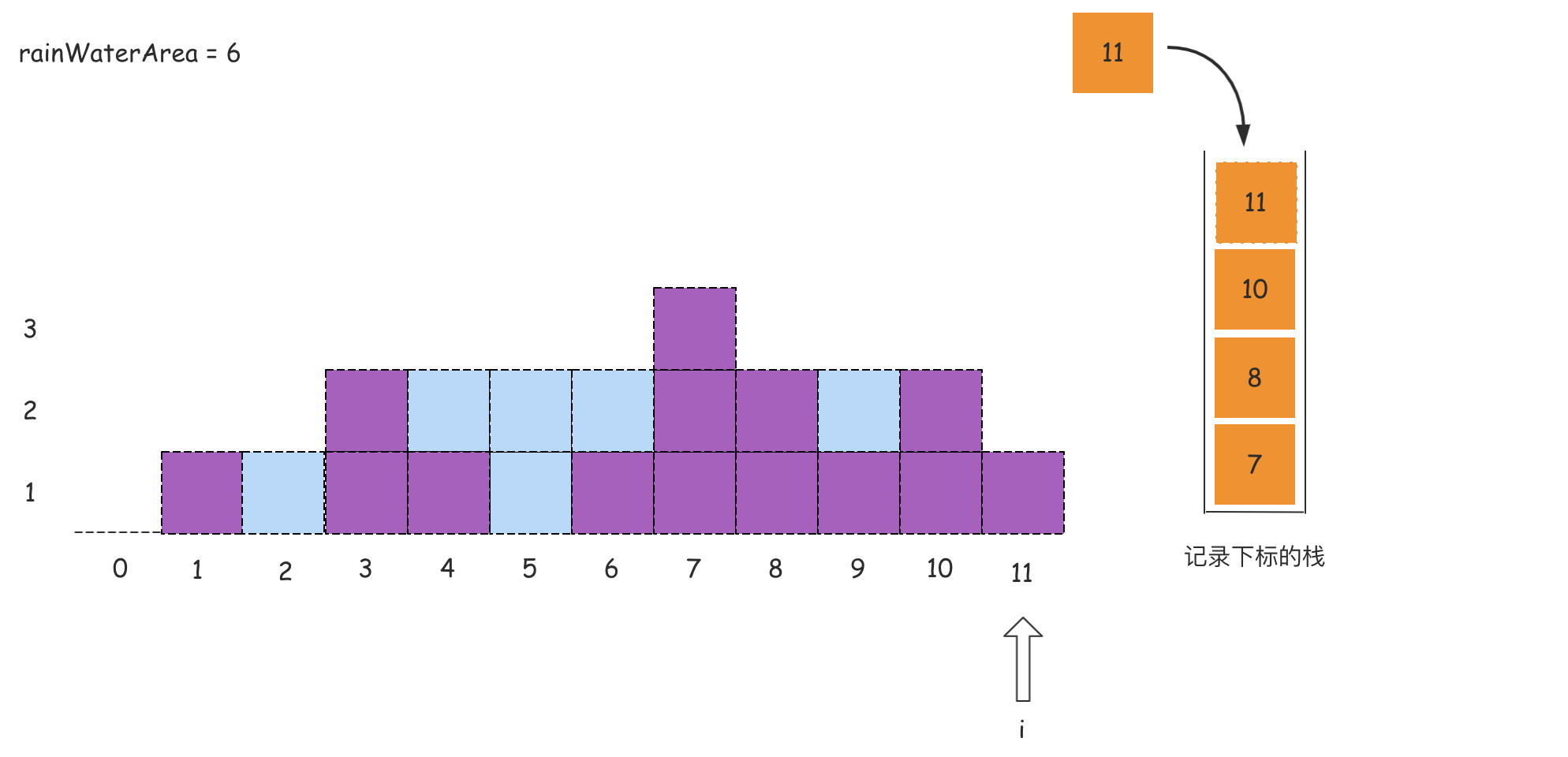
代码如下所示：

/**
 * 单调栈：O(n)
 *
 * @param height 高度数组
 * @return 雨水面积
 */
public int trap(int[] height) {
    // 对于数组个数为0，1，2均无法接到雨水，所以为0
    if (height.length == 0 || height.length == 1 || height.length == 2) {
        return 0;
    }
    // 构建单调递减栈
    Stack<Integer> stack = new Stack<>();
    // 记录雨水面积
    int rainWaterArea = 0;
    for (int i = 0; i < height.length; i++) {
        while (!stack.isEmpty() && height[stack.peek()] < height[i]) {
            int currentIndex = stack.pop();
            if (stack.isEmpty()) {
                break;
            }
            // 获取左边界需要使用peek，而不能使用pop，这是因为需要一层一层计算雨水面积
            int leftIndex = stack.peek();
            int currentHeight = Math.min(height[leftIndex], height[i]) - height[currentIndex];
            rainWaterArea += currentHeight * (i - leftIndex - 1);
        }
        stack.push(i);
    }
    return rainWaterArea;
}

这道题其实很有意思，读者结合代码和上面的图来好好理解，相信定有收货，这里分析一下时间复杂度和空间复杂度，数组的每个元素都被遍历一次，且使用了栈来存储下标，所以时间复杂度是O(n)，空间复杂度也是O(n)。

3.9 去除重复字母 困难

这道题选自leetcode第316题，是一道困难题，但是leetcode将其标记为中等题，不管如何，我们一起来分析下这道题该如何来解决它。

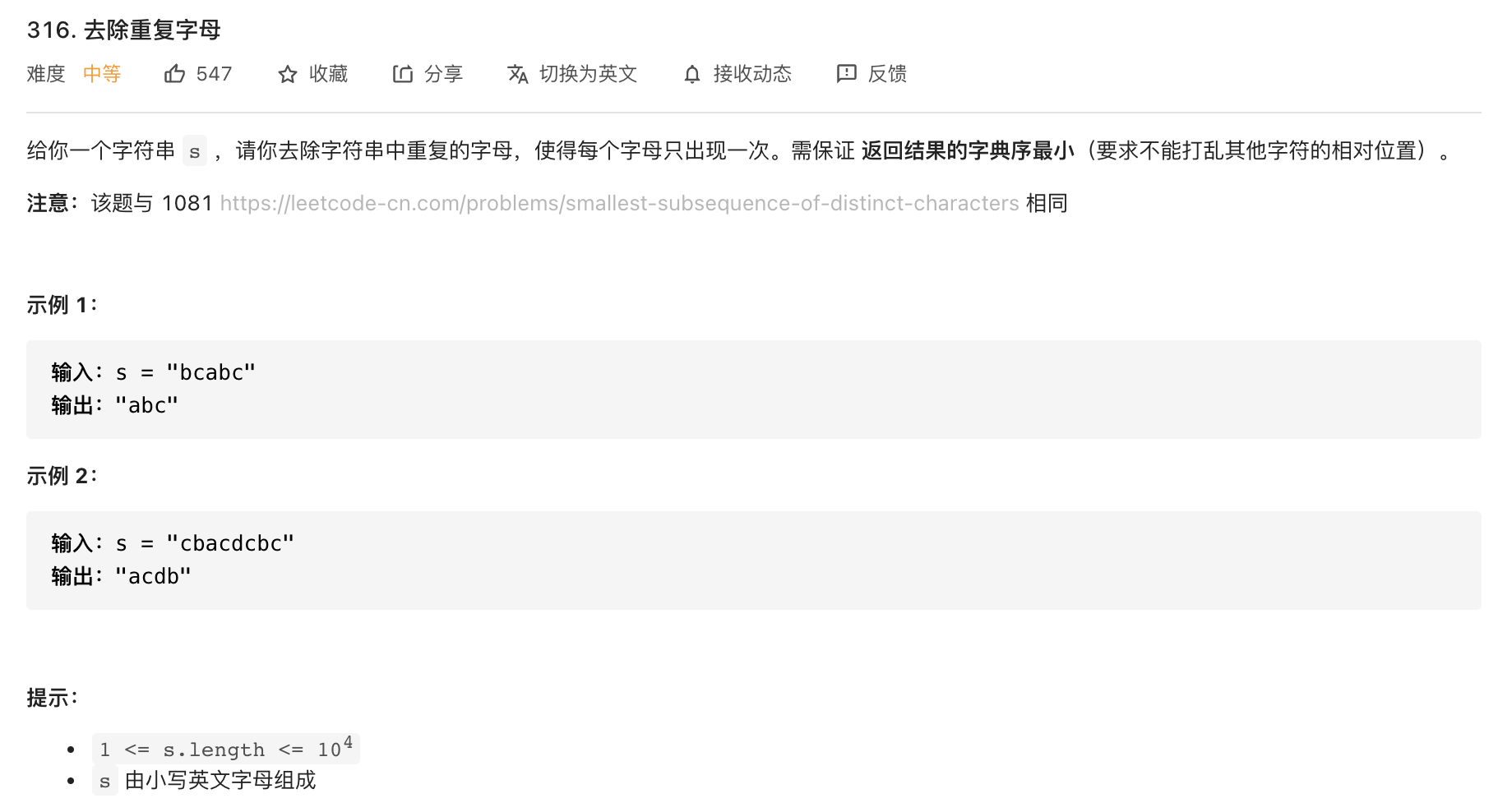
这道题有三个关键点需要注意：

• 去重
• 不能打乱其他字符的相对位置
• 返回结果的字典序最小

我们一点一点来考虑，首先考虑第一点，要求去重，这一点比较简单，常见的做法是遍历字符串的每一个字符，判断字符是否存在于Set中，如果存在，则继续下一个遍历，否则将该字符拼接到新的字符串尾部后再遍历下一个字符，遍历结束，就得到了相对位置不变且去重后的字符串，这种做法满足了上述三个关键点中的前两个。这是去重和保持字符原有相对位置的常见手段，但是对于本题，字符串都是有小写英文字母组成，小写英文字母a ~ z对应的ascii的值是97 ~ 122，所以我们完全可以使用数组+栈来完成去重和保持字符原有相对位置，这里为何使用栈，考虑到后续可能需要构造单调递增栈，字典序最小可以是看作字母从a ~ z的排序。

public String removeDuplicateLetters(String s) {
    // 字符串是小写字母组成，小写字母a~z的ascii的取值范围是97~122
    // 创建一个数组记录栈中是否已经有了该字符，默认值均为false
    boolean[] inStackArray = new boolean[26];
    Stack<Character> stack = new Stack<>();
    for (char c : s.toCharArray()) {
        // 如果字符已经在栈中了，那么就不再进栈了
        if (inStackArray[c % 97]) {
            continue;
        }
        stack.push(c);
        inStackArray[c % 97] = true;
    }
    // 将栈中的元素取出拼成字符串
    StringBuilder sb = new StringBuilder();
    while (!stack.isEmpty()) {
        sb.append(stack.pop());
    }
    return sb.reverse().toString();
}

这段代码使用了数组+栈来解决了去重和保持字符原有相对位置的问题，假如输入的字符串是bcabc，那么输出的结果就是bca，但是这个结果不是题目要求的最终答案，因为题目要求输出的结符合字典序最小，而字典序最小，则结果应该是abc，也就是去重和保持字符原有相对位置的第二个答案。

那如何使结果字典序最小呢？这自然而然就想到了单调递增栈，如果栈顶元素大于当前元素，那么将栈顶元素弹出，直接上代码看的明白：

public String removeDuplicateLetters(String s) {
    // 字符串是小写字母组成，小写字母a~z的ascii的取值范围是97~122
    // 创建一个数组记录栈中是否已经有了该字符，默认值均为false
    boolean[] inStackArray = new boolean[26];
    Stack<Character> stack = new Stack<>();
    for (char c : s.toCharArray()) {
        // 如果字符已经在栈中了，那么就不再进栈了
        if (inStackArray[c % 97]) {
            continue;
        }
        // 构建单调递增栈
        while (!stack.isEmpty() && stack.peek() > c) {
            inStackArray[stack.pop() % 97] = false;
        }
        stack.push(c);
        inStackArray[c % 97] = true;
    }
    // 将栈中的元素取出拼成字符串
    StringBuilder sb = new StringBuilder();
    while (!stack.isEmpty()) {
        sb.append(stack.pop());
    }
    return sb.reverse().toString();
}

同样假设输入的字符串是bcabc，那么输出的结果就是abc，好像是满足了题目的要求？别高兴太早，我们在举个例子，假设输入bcac，那么这个算法输出的结果是ac，但是实际的答案是bac，这很明显不符合要求，其实想起来也很简单，因为我们把唯一的字符b也给弹出了，这明显不符合要求，因为它是唯一的，它不改变相对位置，也不能被去除，所以我们需要有办法统计每个字符出现的次数，对于只有一个的元素，我们不能将其弹出，具体看代码：

/**
 * 单调栈：O(n)
 *
 * @param s 字符串
 * @return 去除重复字母后的字符串
 */
public String removeDuplicateLetters(String s) {
    // 字符串是小写字母组成，小写字母a~z的ascii的取值范围是97~122
    // 创建一个26个英文字母的数组来记录每个小写字母出现的次数
    int[] count = new int[26];
    for (char c : s.toCharArray()) {
        count[c % 97]++;
    }
    // 创建一个数组记录栈中是否已经有了该字符，默认值均为false
    boolean[] inStackArray = new boolean[26];
    Stack<Character> stack = new Stack<>();
    for (char c : s.toCharArray()) {
        // 每遍历一个字符，该字符出现的次数就少一次
        count[c % 97]--;
        // 如果字符已经在栈中了，那么就不再进栈了
        if (inStackArray[c % 97]) {
            continue;
        }
        // 构建单调递增栈
        while (!stack.isEmpty() && stack.peek() > c) {
            if (count[stack.peek() % 97] == 0) {
                break;
            }
            inStackArray[stack.pop() % 97] = false;
        }
        stack.push(c);
        inStackArray[c % 97] = true;
    }
    // 将栈中的元素取出拼成字符串
    StringBuilder sb = new StringBuilder();
    while (!stack.isEmpty()) {
        sb.append(stack.pop());
    }
    return sb.reverse().toString();
}

这段代码就完成覆盖了题目的要求了，读者可以一点点读这个写代码的过程，相信大家肯定可以读懂。这里需要说明一点，c % 97是计算了字符c（它是个变量，代表任意小写字母）在数组的相对位置，a在ascii中是97，所以a % 97 = 0，也就是数组的第一个位置，0号位置。

分析一下时间复杂度和空间复杂度，都是对数组进行一次遍历，空间使用也是元素个数的常数倍，所以时间和空间复杂度都是O(n)。

四、最后

leetcode中几道常见的单调栈问题都在这里了，把这几道题做好了，相信单调栈的问题将不再是难题。各位读者加油💪🏻