第2节数组的二分查找算法

学习了第1节数组理论基础，相信读者已经对数组这种基本数据结构有了基本的认识，接下来，我们通过一个案例入手，一起学习一下数组的『二分查找』算法。

一、经典案例

这里给定一个基础案例，这个案例其实就是 leetcode在新窗口打开上的 第704题 ，题目内容如下所示：

描述：

给定一个 $n$ 个元素有序的（升序）整型数组 $nums$ 和一个目标值 $target$ ，写一个函数搜索 $nums$ 中的 $target$ ，如果目标值存在返回下标，否则返回 $-1$ 。

示例1：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例2：

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 $nums$ 中的所有元素是不重复的。
$n$ 将在 $[1, 10000]$ 之间。
$nums$ 的每个元素都将在 $[-9999, 9999]$ 之间。

看到这道题，我们第一感觉就是很简单，没错，它在 leetcode 上被标注为一道简单题，正常情况下，刚开始接触 leetcode 的时候，我们往往会去遍历它，通过遍历可以很快将目标元素的下标给输出出来，我们一起来看一下下面的图，并写出代码。

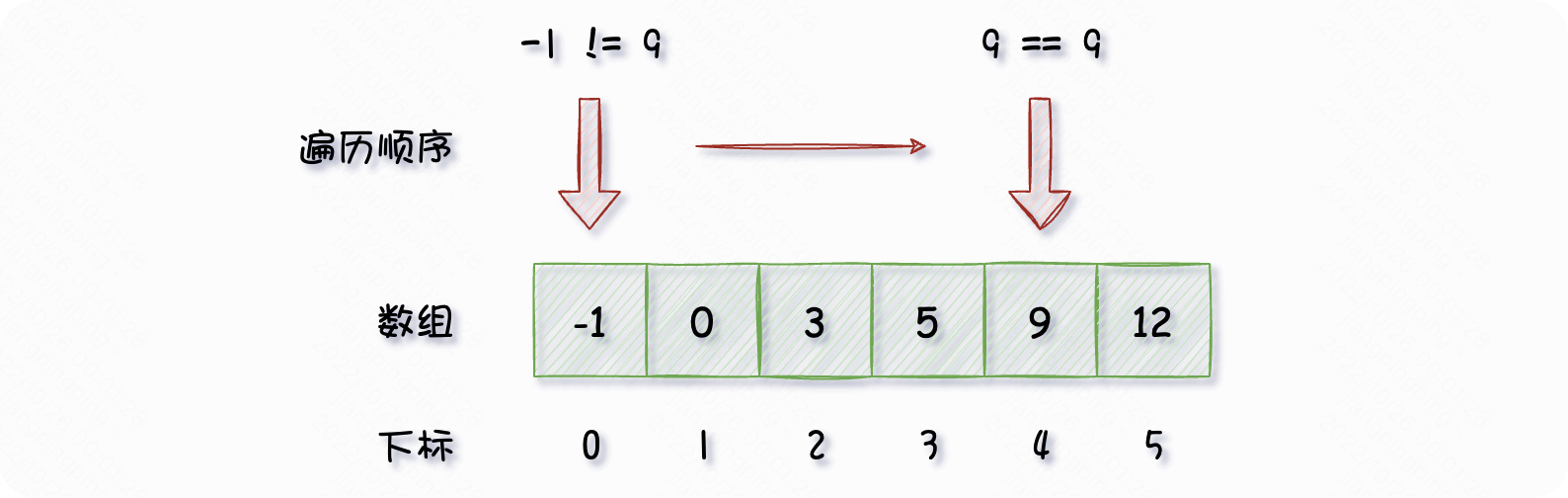
上图描述的很清晰，我们从左往右进行遍历：第一个元素 -1 不等于 9 ，接下来遍历第二个元素 0 ，它同样不等于 9 ，继续往后遍历，当遍历到第五个元素的时候，发现它等于 9 ，那么返回它的下标为 4 。

要在上述数组中查找元素 2 ，也是采用同样从左往右的方式，发现数组中并没有等于 2 的元素，那么遍历结束后，直接返回 -1 。

通过图文的描述，我相信读者已经理解了，我们这里直接写出代码：

class Solution {
    public int search(int[] nums, int target) {
        // 对每一个元素进行遍历
        for (int i = 0; i < nums.length; i++) {
            // 如果数组中某个元素等于目标元素，则直接返回元素下标
            if (target == nums[i]) {
                return i;
            }
        }
        
        // 如果不存在目标元素，直接返回-1
        return -1;
    }
}

复杂度分析：

时间复杂度： $O(n)$
空间复杂度： $O(1)$

我们做完这一道题，也分析了时间复杂度，那么有办法降低这个时间复杂度吗？或者说，有更优的解法吗？答案是当然有，它就是本节的重点要介绍的解法： 二分查找法 。

二、二分查找算法

2.1 什么是二分查找

何为 『二分查找』 ？相信刚刚接触数据结构与算法的读者可能会懵，不急，我举个生活中出现过的例子，相信这类读者肯定会很快明白。

以前看过一档综艺节目，主持人手中有 100 牌，每张牌中都有一个数字，数字分别是从 1 到 100 ，主持人让嘉宾随机抽取一张，然后主持人要在极短的时间内猜中嘉宾抽中的牌是哪一个数字（假设本次读者抽中的是 79 ），主持人不可以直接问嘉宾牌上数字是多少，嘉宾只用回答 是 或者 不是 ，那么这个时候，他们之间的对话就开始了。

主持人： “您手中的牌数字大于 50 吗？”

嘉宾： “是”

主持人： “您手中的牌数字大于 75 吗？”

嘉宾： “是”

主持人： “您手中的牌数字大于 88 吗？”

嘉宾： “不是”

主持人： “您手中的牌数字大于 81 吗？”

嘉宾： “不是”

主持人： “您手中的牌数字大于 78 吗？”

嘉宾： “是”

主持人： “您手中的牌大于 79 吗？”

嘉宾： “不是”

主持人： “我猜出来了，您手中的牌数字是 79 ！”

嘉宾： “恭喜您，答对了！”

相信这个综艺节目的这种案例大家都看过或者听过，主持人在问了嘉宾六个问题后，第七次就直接猜中了嘉宾抽取的牌数字。如果说，主持人从数字 1 开始挨个问：“您牌的数字是不是 1 ...”，那么他需要问 79 次才能问中，假设主持从 100 倒序往前问，也得问 21 次才可以问到答案。

其实，主持人这种问法，正是经典的 『减而治之』 的思想，也是 『二分查找算法』 的应用。 『减而治之』 思想就是：一步步缩小问题范围，在小范围中去解决问题。主持人通过问嘉宾手中的牌数字是否比某个值大，从而来缩小范围，最终确定了范围是 $[79, 80]$ ，那么通过最后一个问题直接判断出答案是 79 。

我们将 1 ~ 100 的牌理解为 $[1, 2, 3, ..., 99, 100]$ 的数组，那么我们再来思考下何为 『二分查找』 ，相信读者肯定就容易理解多了。顾名思义，就是将数组一分为二，排除掉不可能的二分之一数组，继续从剩下二分之一数组中去查找，这种查找算法最基本的条件就是数组要有序，它是一种在有序数组中查找某一特定元素的搜索算法。二分查找算法的叫法也很多，常见的有： 折半查找算法 、 对半查找算法 、 对数查找算法 等。

上面的综艺节目的案例，其实是 『二分查找算法』 的 排除法 的应用，主持人没有直接问：“您手中的牌等于 xx 吗？你手中的牌大于 xx 吗？”，而是只是问是否大于某个数，这样问是直接排除了不可能的区间，直到最后只剩下一个元素，直接判断最后剩下的元素是否等于目标元素即可。其实还有一种思路，那就是 主动找 ，它类比下来就是主持人会问两个问题：“您手中的牌等于 xx 吗？你手中的牌大于 xx 吗？”，首先通过问是否等于某个数来 主动找 ，这是 『二分查找算法』 里常见的思路，理解起来比 排除法 思路还简单一些。它的基本过程如下：

拿到一个数组（默认数组有序）以后，直接找到数组的中间元素，如果中间元素正好等于目标元素，则搜索过程结束，直接返回中间元素的下标即可；
如果目标元素大于（小于）中间元素，则在数组大于（小于）中间元素的那一半中查找，而且跟开始一样，从中间元素开始比较；
如果找到最后，数组为空了，则代表找不到，返回 -1 即可。

对于这种 主动找 的思路，我也来举个例子，给定一个有序数组 $[1, 2, 4, 16, 17, 19, 20, 21, 23, 31, 39]$ ，我们需要判断 21 是否在数组中，如果在，返回它在数组中的下标，如果不在，直接返回 -1 。

我们根据上面 主动找 的基本过程来看如何使用 『二分查找算法』 来快速找到结果：

首先找到中间元素 19 ，它不等于 21 ，因为 21 比 19 大，所以，我们需要在大于 19 的那一半去接着找，此时寻找区间变成了 $[20, 21, 23, 31, 39]$ ；
我们在 $[20, 21, 23, 31, 39]$ 这一半找到中间元素 23 ，它不等于 21 ，它比 21 大，所以我们需要到小于 23 的那一半去接着找，此时寻找区间变成了 $[20, 21]$ ；
此时寻找空间就剩下两个元素，我们找中间元素，元素 20 的下标是 6 ，元素 21 的下标是 7 ，我们取两个下标之和除以 2 ，在计算机整型中除以有向下取整的过程， $13 / 2 = 6$ ，所以中间元素为 20 ，此时继续判断 21 大于 20 ，所以需要在 20 右边区间继续寻找，此时寻找区间变成了 [21] ；
最后一步，自然而然， 21 成为了中间元素，它等于目标元素，所以此时找到了结果，返回 21 的下标为 7 。

我们通过 『二分查找算法』 来搜索元素，只搜索了 4 次就找到了目标元素，如果挨个儿遍历，那也需要遍历 8 次才能找到，所以说， 『二分查找算法』 是比普通遍历更优的算法。

2.2 使用语言实现二分查找算法

我们还是以第一小节中的经典案例来举例，我们这次尝试使用二分查找算法来解决这个搜索问题。首先，我们还是通过画图的形式，将过程展示出来，过程理清楚了，代码写起来就不难了，图文过程如下所示：

首先我们定义三个变量：

$left$ ：左边界下标
$right$ ：右边界下标
$mid$ ：中间值下标

初始值设置为： $left = 0$ ， $right = nums.length - 1$ ， $mid = (left + right) / 2$

数组的搜索区间为 $[left, right]$ ，中间值的下标为 $mid$ ，我们按照 主动找 的思路来解决这个问题，基本步骤如下：

如果中间位置值 $nums[mid]$ 与目标值 $target$ 相等，则返回中间值下标；
如果中间位置值 $nums[mid]$ 小于目标值 $target$ ，说明如果目标值存在，则一定在中间值的右区间，此时将左边界设置为 $mid + 1$ ，然后继续在右区间 $[mid + 1, right]$ 中搜索；
如果中间位置值 $nums[mid]$ 大于目标值 $target$ ，说明如果目标值存在，则一定在中间值的左区间，此时将右边界设置为 $mid - 1$ ，然后继续在左区间 $[left, mid - 1]$ 中搜索。

转换成图形式如下所示：

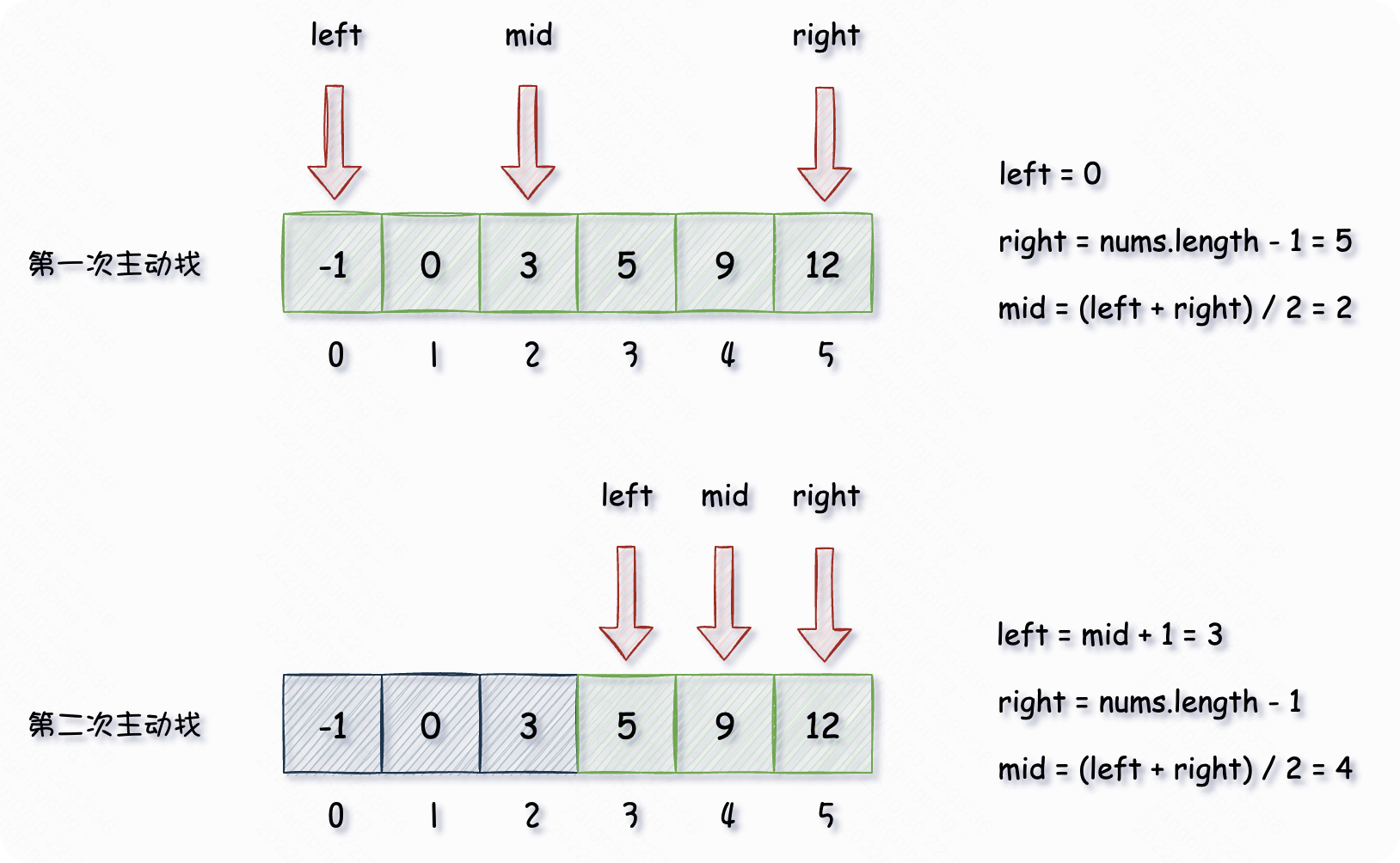
从上面的图文可以看出，我们通过 2 次就找到了目标值，效率是杠杠的！

我们一起来看下代码如何实现，这里直接给出代码如下：

class Solution {
    public int search(int[] nums, int target) {
        // 定义三个变量
        int left = 0;
        int right = nums.length - 1;
        int mid;

        // 跳出循环的条件是 left > right，当left == right的时候，是最后一次循环，此时待查找区间只剩下一个元素
        // 如果最后一个元素不等于目标元素，说明数组nums里面不含目标元素，直接返回 -1
        while (left <= right) {
            mid = (left + right) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        // 如果不存在目标元素，直接返回-1
        return -1;
    }
}

复杂度分析：

时间复杂度： $O(\log_{2}{n})$ ，这里 $n$ 是输入数组的长度
空间复杂度： $O(1)$

2.3 二分查找中的细节分析

『二分查找算法』 的原理很简单，但是其中的细节是需要读者彻底弄明白，否则也是很容易出问题的，只有原理和细节都掌握了，那么对于这类算法题，解起来将得心应手。

这里列举 4 个大家常见的细节问题：

搜索区间的开闭问题： 在定义区间变量的时候，是选择 左闭右闭 （也就是 [ ] ）还是 左闭右开 （也就是 [ ) ）？
中间值下标取值问题： 取 $mid = (left + right) / 2$ 还是 $mid = left + (right - left) / 2$ ？
判断条件设置问题： 判断条件该选 $left <= right$ 还是 $left < right$ ？
搜索区间选择问题： 区间边界选择也有多种组合，常见的有 $left = mid + 1$ 、 $right = mid - 1$ 和 $left = mid + 1$ 、 $right = mid$ ，那么该选择哪一对组合呢？

是不是我这么一列举，你瞬间觉得自己又整不会啦？没关系，我们一起来一一分析一下这四个问题，分析清楚了，理解了，做题的时候才不会懵。

2.3.1 搜索区间的开闭问题

在数组操作中，都要考虑边界问题，数组不能越界，比如数组长度为 3 ，它的元素下标分别为 0, 1, 2 ，那么在取元素的时候，是取不到下标为 3 的元素的，因为它越界了。有了这个基础，我们来看看常见的两种边界定义方式：

左闭右闭：左右边界都是有意义的， $left = 0$ 、 $right = nums.length - 1$ 分别是数组 $nums$ 的左边界和右边界， $left$ 是 $nums$ 的第一个元素， $right$ 是 $nums$ 最后一个元素，它的表示方式是 $[left, right]$ 。
左闭右开：左边边界是有意义的，右边边界是超出数组的最后一个下标的，它是数组最后一个元素的下一个位置，左边边界是可以取到的，但是右边边界是取不到的， $left = 0$ 、 $right = nums.length$ ，它的表示方式是 $[left, right)$ 。

如果上面的案例选择 左闭右开 的搜索区间，那么右边的值是始终取不到的，即不存在 $left == right$ 的情况，这个时候判断条件就需要有对应的变化，判断条件应该为 $left < right$ ，那么它退出循环的条件就是 $left == right$ ，换句话说，当 $left = right - 1$ 的时候，搜索区间就剩最后一个元素了，如果最后一个元素不是目标元素，那么说明整个数组中不包含目标元素，相应的代码如下所示：

class Solution {
    public int search(int[] nums, int target) {
        // 定义三个变量
        int left = 0;
        int right = nums.length;
        int mid;

        // 跳出循环的条件是 left == right，当left = right - 1的时候，是最后一次循环，此时待查找区间只剩下一个元素
        // 如果最后一个元素不等于目标元素，说明数组nums里面不含目标元素，直接返回 -1
        while (left < right) {
            mid = (left + right) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                // 右边是单开，所以只能是mid，不是mid - 1
                right = mid;
            }
        }

        // 如果不存在目标元素，直接返回-1
        return -1;
    }
}

这两种区间都可以选择，但是最常见的还是 左闭右闭 ，读者在做 leetcode 算法题的时候，熟练掌握其中一种即可，整体推荐 左闭右闭 。

2.3.2 中间值下标取值问题

关于中间值下标 $mid$ 的取值，很多读者也挺迷惑，为什么迷惑呢，主要原因还是看了太多版本的解析了，常见的写法有好几种，看得读者眼花缭乱，始终弄不清楚该选择哪一种了，其实是没有弄明白其中的原理，咱们接下来列举常见的几种写法，并谈一谈它的原理， $mid$ 常见的取值方式如下所示：

第一种： 向下取整，取左边。

意思就是说当数组的个数是偶数的时候，它取中间值的时候，以下两种常见写法都是取左边的，例如数组 $[1, 2, 3, 4, 5, 6]$ ，它的中间值用下面两种计算方法，取的中间值是 3 ，而不是 4 。计算方式是 $mid = (0 + 5) / 2 = 2$ ， $mid = 0 + (5 - 0) / 2 = 2$ ，计算公式如下：

$mid = (left + right) / 2$
$mid = left + (right - left) / 2$

这两种计算方式有何不同呢？其实在小范围内也没什么不同，第一个大家很好理解，就是首尾相加除以 2 ，第二个写法，是为了防止整型溢出，什么意思呢？我以 Java 举例， Integer 类型的最大值是 2147483647 ，假设某个数组最后一个元素的下标正好为 2147483647 ，假设要寻找某个目标元素，它在整个数组的右半部分，此时当 $left$ 设置为中间值的下标的时候，再次计算 $mid$ 的时候，中间值下标和 2147483647 相加肯定会超过 Integer 类型的最大值，此时程序会报错，此时第二种写法就成为了第一种写法的替代者，它不会造成整型溢出。所以在处理 leetcode 问题的时候，考虑使用哪种方式，取决于数组的最后一个元素下标会不会造成整型溢出，如果不会造成，为了问题简单化，我推荐第一种写法，如果你想求稳，第二种写法适合你。

第二种： 向上取整，取右边。

可能有读者会问，取右边可以吗，当然可以。想取右边，只需要稍微变动一下公式即可，如下所示：

$mid = (left + right + 1) / 2$
$mid = left + (right - left + 1) / 2$

读到这里，其实大家应该能理解，二分查找，并不一定取值一定是在正中间，靠左一点，靠右一点都是可以的，关键是需要理解取值的方式之间的区别即可。

这里发散一下思维：既然有 『二分查找算法』 ，那么是否可以有 『三分查找算法』 、『四分查找算法』 甚至是 『五分查找算法』 ，其实是可以有的，假设使用 『五分查找算法』 ，如果目标元素在前五分之一，那么效果是比二分查找要好的，其实这也是一种“赌博”的心态，总体来说，二分查找算法更加稳定。

2.3.3 判断条件设置问题

在二分查找中，对于判断条件的写法，常见的通常有两种：

$left <= right$
$left < right$

至于该选择哪个，其实和区间的开闭有关系，我们针对 左闭右闭 和 左闭右开 这两种区间类型都分析一下，接下来的内容不需要记忆，只需要理解即可，理解后，无论哪种区间类型，都能正确地应用判断条件。

在 左闭右闭 的区间类型下：

如果选择 $left <= right$ ，那么判断语句的结束条件就是 $left == right + 1$ ，此时左边界比右边界还大，这样的查找空间是不存在的，比如 $[3, 2]$ ，待搜索的区间中没有任何元素存在，此时直接返回 $-1$ 即可。这个示例代码直接参考上面 2.2 的内容即可。

如果选择 $left < right$ ，那么判断语句的结束条件 $left == right$ ，此时左右边界相等，此时搜索区间中其实还有一个元素，此时直接返回 $-1$ 是不对的，因为漏掉了一个元素没有进行对比，区间 $[right, right]$ 是有意义的。如果非要使用这个判断条件，那么应该在跳出循环后，再做一次判断，判断目标元素是否等于 $nums[left]$ ，如果等于，则返回 $left$ ，否则返回 $-1$ 。这个示例代码如下所示：

class Solution {
    public int search(int[] nums, int target) {
        // 定义三个变量
        int left = 0;
        int right = nums.length - 1;
        int mid;

        // 跳出循环的条件是 left == right，当left = right - 1的时候，是最后一次循环，此时待查找区间只剩下两个元素
        // 检查完 right - 1 的元素后，就跳出了，少检查了一个 right的元素，也就是这种判断条件在循环体中漏掉了一个元素
        while (left < right) {
            mid = (left + right) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        // 最后还要检查循环体没有检查的元素才能得出正确结果
        return nums[left] == target ? left : -1;
    }
}

在 左闭右开 的区间类型下：

选择 $left <= right$ 是没有意义的，因为 $right$ 这个下标是已经超过搜索区间的最右边的元素下标了，所以只应该选择 $left < right$ ，此时当循环到 $left == right - 1$ 的时候，已经是最后一次循环了，如果最后一次循环还找不到目标元素，那么直接返回 $-1$ 。这个场景的案例代码请参考上面 2.3.1 即可。

2.3.4 搜索区间选择问题

循环过程中，有一个绕不过去的问题，那就是左右边界的重新赋值问题，其实它就是搜索区间的选择问题，常见的组合有 $left = mid + 1$ 、 $right = mid - 1$ 和 $left = mid + 1$ 、 $right = mid$ ，甚至还有 $left = mid$ 、 $right = mid - 1$ 等。

区间选择的问题，一定要搞清楚，中间元素的下标是否需要包含进来，例如：

如果你采用的是 主动找 的思路，且应用的是 左闭右闭 ，那么你会判断一下中间元素是否等于目标元素，然后根据中间元素与目标元素的大小来确定左右边界，如果目标元素大于中间元素，那么目标元素如果存在，一定在中间元素的右边，此时肯定有 $left = mid + 1$ ，且此时 $right$ 不动；如果目标元素小于中间元素，那么目标元素如果存在，一定在中间元素的左边，此时肯定有 $right = mid - 1$ ，且此时 $left$ 不动。如果你应用的是 左闭右开 ，那么一定是 $left = mid + 1$ 和 $right = mid$ 的组合，因为左侧边界是不包括的。
如果你采用的是 排除法 的思路，且应用的是 左闭右闭 ，那么你不会去判断中间元素是否和目标元素相等，你只会问中间元素是否大于目标元素，如果大于，自然左边界就是 $left = mid + 1$ ，右边界 $right$ 不动，如果不是大于，那么肯定就是小于等于，此时左边界 $left$ 不动， $right = mid$ ，且 $mid$ 元素是不能漏掉的。

这四个细节问题不能单独去谈，要放到一起去分析，关于这些问题的讨论，无需去记忆，只需要理解即可，遇到类似的问题，可以按照上述的理解去思考，去找到解决办法。

2.4 排除法思路介绍

这里也简单地实现 排除法 思路，它与 主动找 的区别就是它不去比较是否相等，只比较大小，然后按照排除区间的形式来一步步缩小搜索区间，最后只需要判断最后一个元素是否等于目标元素即可，这个思想就和上述“综艺节目”一样。这里仅贴出代码，读者自行思考其中的奥秘。

class Solution {
    public int search(int[] nums, int target) {
        // 定义三个变量
        int left = 0;
        int right = nums.length - 1;
        int mid;

        // 跳出循环的条件是 left == right，当 left = right - 1 的时候，是最后一次循环，此时待查找区间只剩下两个元素
        // 检查完 right - 1 的元素后，就跳出了，少检查了一个 right的元素，也就是这种判断条件在循环体中漏掉了一个元素
        while (left < right) {
            mid = (left + right) / 2;
            if (target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        // 排除完所有区间后，还剩最后一个元素，直接对比出结果
        return nums[left] == target ? left : -1;
    }
}

三、精选练习题

我们一起学习了二分查找算法基本原理，也分析了二分查找中的细节问题，接下来，我们精选几道 leetcode 上算法题来巩固一下。

题号	题目	难度	题解	解析
374	猜数字大小在新窗口打开	简单	Java	3.1
35	搜索插入位置在新窗口打开	简单	Java	3.2
34	在排序数组中查找元素的第一个和最后一个位置在新窗口打开	中等	Java	3.3
69	x 的平方根在新窗口打开	简单	Java	3.4
287	寻找重复数在新窗口打开	中等	Java	3.5
50	Pow(x, n)在新窗口打开	中等	Java	3.6

3.1 猜数字大小简单

原题链接：猜数字大小在新窗口打开

描述：

猜数字游戏的规则如下：

每轮游戏，我都会从 $1$ 到 $n$ 随机选择一个数字。请你猜选出的是哪个数字。
如果你猜错了，我会告诉你，你猜测的数字比我选出的数字是大了还是小了。

你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果，返回值一共有 $3$ 种可能的情况（ $-1$ ， $1$ 或 $0$ ）：

$-1$ ：我选出的数字比你猜的数字小 $pick < num$
$1$ ：我选出的数字比你猜的数字大 $pick > num$
$0$ ：我选出的数字和你猜的数字一样。恭喜！你猜对了！ $pick == num$

返回我选出的数字。

示例 1：

输入：n = 10, pick = 6
输出：6

示例 2：

输入：n = 1, pick = 1
输出：1

示例 3：

输入：n = 2, pick = 1
输出：1

示例 4：

输入：n = 2, pick = 2
输出：2

提示：

$1 <= n <= 2^{31} - 1$
$1 <= pick <= n$

思路分析：

读完这道题，是否感觉这道题和本文上述 主持人猜数 的案例一模一样呀？没错，它们原理和流程都是一样的，只不过这次，主持人问：“您手中的牌是50！”，嘉宾回答的提示更加丰富，他不仅会告诉你猜对了没有，还会告诉你猜的数是大了还是小了，这不是正好可以使用 主动找 的思想来解决这个问题？

我们一起将题目转换成熟悉的数组类问题：

已知一个连续且递增数组 $[1, ..., n]$ ，目标元素一定存在于其中，请找出目标元素。接口 int guess(int num) 已经定义好了，你只需要调用即可，传入你想要猜的数字，它会告诉你猜对了没有，或者告诉你猜大了或者猜小了。如果猜对了，接口将返回 $0$ 给你，如果你猜的数字大于目标值，那么它将返回 $-1$ 给你，如果你猜的数字小于目标值，那么它将返回 $1$ 给你。

这么转换后，相信题目更加好理解了，目标值虽然没有明确告诉你，但是提供一个预定义的接口，通过接口返回值，就能知道所选值与目标值的大小关系，其实就是将和目标值比较的过程交给了预定义的接口 int guess(int num) ，有了这样一个背景，我们很容易解决这道题了。

我们以 示例1 来作为画图的案例，定义变量：

int left = 0;
int right = nums.length - 1;
int mid;

图解过程如下：

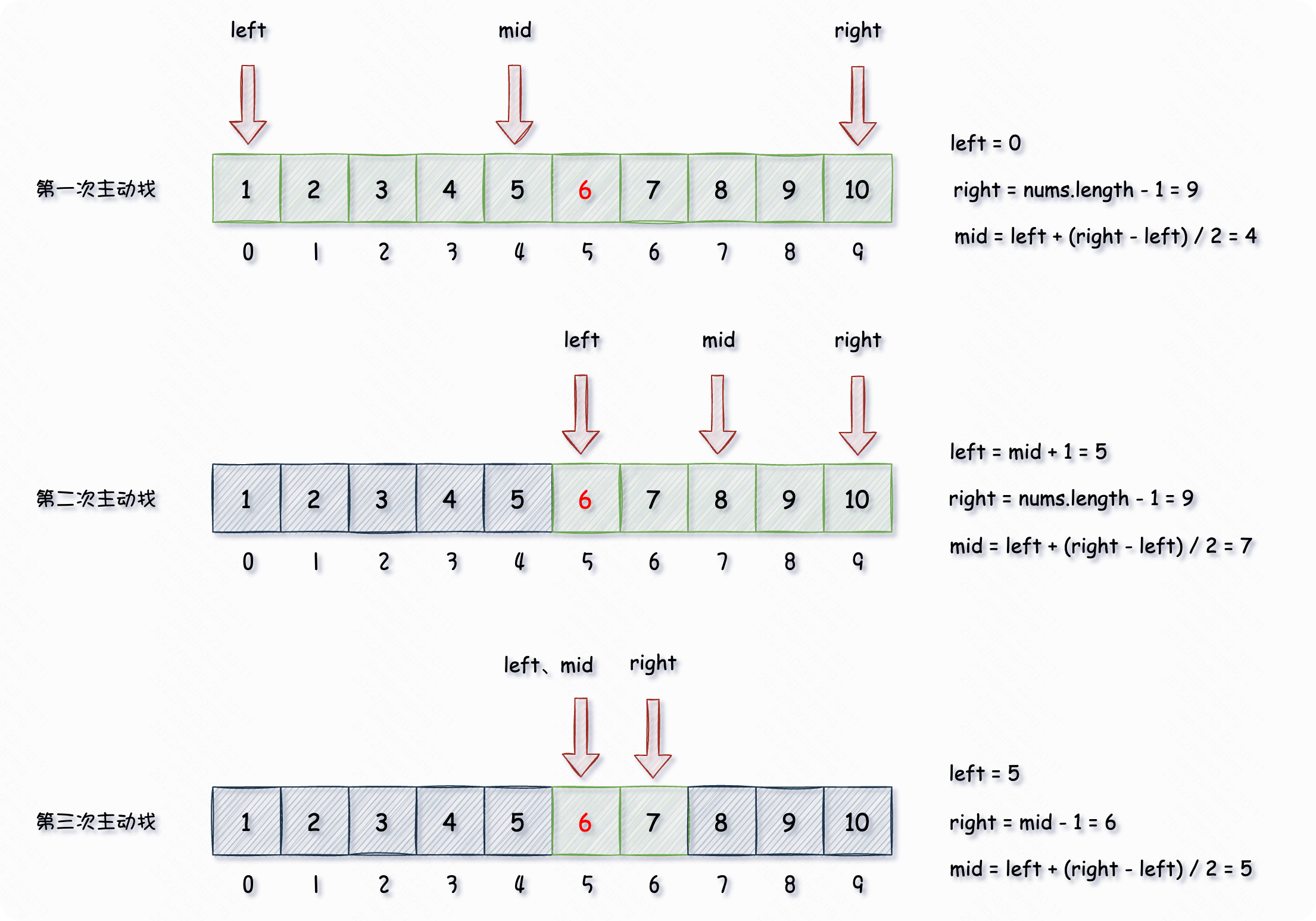
特别注意：

我们将题目转换成数组的形式来表示，那么本题需要重点关注的一个问题就是，数组元素下标与元素的关系要弄清楚，数组的元素比下标大 $1$ ，也就是说下标加 $1$ 就是对应的元素的值，这一点很重要。
这道题有个特殊之处，那就是数组是从 $1$ 开始连续以 $1$ 来递增的一种数组，如果我们弄清楚了下标与元素的关系，其实我们可以认为下标是从 $1$ 开始的（实际是从 $0$ 开始），这样的话下标和元素就是相等的了，这样的思想也可以处理这道题。未来很多时候，解其他题目的时候，都会使用这种思想，读者需要认真理解。

这两个需要特别注意的点，就诞生了两种常见的解法，我们这里直接贴出代码，如下所示：

代码展示：

public class Solution extends GuessGame {
    public int guessNumber(int n) {
        // 定义三个变量，它们分别是待搜索区间的左边界、右边界及中间值下标
        int left = 0;
        int right = n - 1;
        int mid;

        // 退出循环的条件是 left == right，此时说明待搜索区间只剩下一个元素，一定就是目标元素
        while (left < right) {
            mid = left + (right - left) / 2;
            // 中间值
            int midValue = mid + 1;
            if (guess(midValue) == 0) {
                // 猜对了，直接返回中间值
                return midValue;
            } else if (guess(midValue) < 0) {
                // 猜大了，说明目标值在区间[left, mid - 1]这个区间内
                right = mid - 1;
            } else {
                // 猜小了，说明目标值在区间[mid + 1, right]这个区间内
                left = mid + 1;
            }
        }

        // 能走到这里，此时说明待搜索区间只剩下一个元素，一定就是目标元素
        return left + 1;
    }
}

public class Solution extends GuessGame {
    public int guessNumber(int n) {
        // 定义三个变量，这里简单认为数组的下标从1开始，它们分别是待搜索区间的左边界、右边界及中间值下标
        int left = 1;
        int right = n;
        int mid;

        // 退出循环的条件是 left == right，此时说明待搜索区间只剩下一个元素，一定就是目标元素
        while (left < right) {
            mid = left + (right - left) / 2;
            if (guess(mid) == 0) {
                // 猜对了，直接返回中间值
                return mid;
            } else if (guess(mid) < 0) {
                // 猜大了，说明目标值在区间[left, mid - 1]这个区间内
                right = mid - 1;
            } else {
                // 猜小了，说明目标值在区间[mid + 1, right]这个区间内
                left = mid + 1;
            }
        }

        // 能走到这里，此时说明待搜索区间只剩下一个元素，一定就是目标元素
        return left;
    }
}

复杂度分析：

时间复杂度： $O(\log_{2}{n})$ ，这里 $n$ 是输入数组的长度
空间复杂度： $O(1)$

这里解释一下两种解法中 mid 值和判断条件的思路：

$mid = left + (right - left) / 2$ ：这里之所以这么写，是为了防止整型溢出，因为题目中标记了 $n$ 的范围是： $1 <= n <= 2^{31} - 1$ ，所以如果写成 $mid = (left + right) / 2$ ，是有溢出的可能性的。
解法中判断条件写的 $left < right$ ，它的退出循环的条件是 $left == right$ ，此时如果退出循环的话，一定满足该条件，此时直接返回该小标对应的值即可。

3.2 搜索插入位置简单

原题链接：搜索插入位置在新窗口打开

描述：

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。请必须使用时间复杂度为 $O(log n)$ 的算法。

示例 1：

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2：

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3：

输入: nums = [1,3,5,6], target = 7
输出: 4

提示：

$1 <= nums.length <= 104$
$-104 <= nums[i] <= 104$
$nums$ 为 无重复元素 的升序排列数组
$-104 <= target <= 104$

思路分析：

我们阅读到题目，从 排序数组 、 目标值 、 $O(log n)$ 等关键字中就可以看出，本道算法题适合使用二分查找算法来做。这道题和别的二分查找算法有点点变异，如果没有找到目标值，那么需要将目标值插入到数组中，并返回目标值的下标。虽然说是要插入目标值，其实不用真的原数组将目标值插入，只需要返回目标值的下标即可。

这里，其实有两种情况，

第一种是目标值存在于数组中，那么直接通过二分查找可以很快找到目标值；
第二种情况是目标值不存在于数组中，我们需要找到合适的位置来安放目标值。

对于第一种情况，我们已经很熟悉，第二种情况，我们一起来分析一下，这里也通过一个图文的形式来讲解，这里以 示例2 作为例子。

定义变量：

int left = 0;
int right = nums.length - 1;
int mid;

图解过程如下：

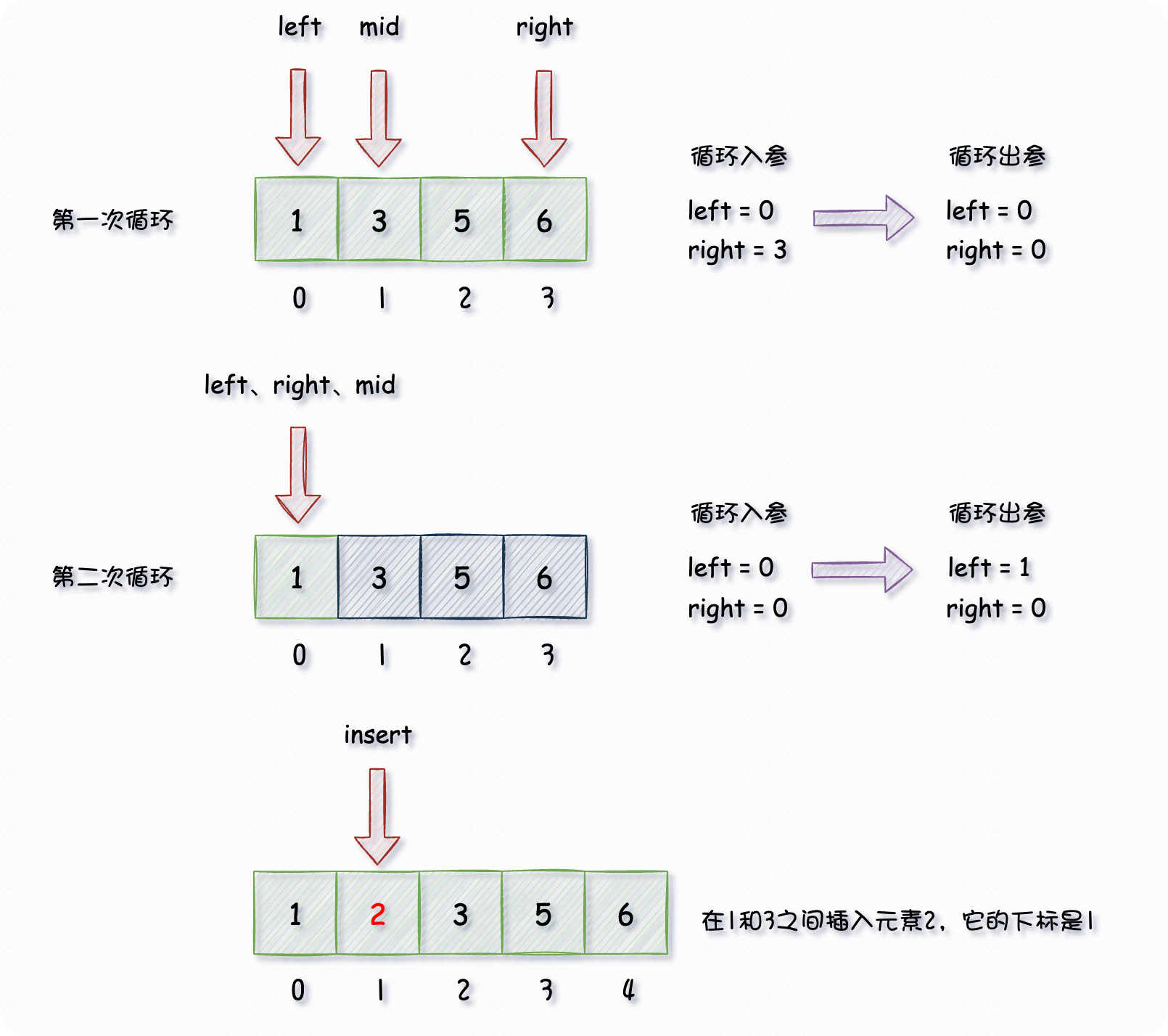
我们从图中可以看出，第一次循环，入参是：

int left = 0;
int right = nums.length - 1 = 3;
// 计算出mid
int mid = 1;

由于目标值 $2$ 小于 $nums[mid]$ ，目标值如果存在，必定在 $[0, mid - 1]$ 这个区间，此时进入到第二次循环中，此时入参是：

int left = 0;
int right = 0;
// 计算出mid
int mid = 0;

此时由于目标值 $2$ 大于 $nums[mid]$ ，目标值不存在，且目标值在 $nums[mid]$ 右边，此时目标值的索引为 $mid + 1$ ，也就此时的 $left$ 变量的值。

我们假设目标值 $2$ 小于 $nums[mid]$ ，那是需要在 $nums[mid]$ 左边插入目标值元素，此时相当于 $nums[mid]$ 向右边右移了一个位置，将 mid 位置让给了目标值，此时就知道目标值的位置就是 $mid$ ，也就是此时的 $left$ 变量的值。

根据图文的分析，我们直接给出代码如下所示：

代码展示：

class Solution {
    public int searchInsert(int[] nums, int target) {
        // 定义三个变量，它们分别是左右边界及中间值的下标
        int left = 0;
        int right = nums.length - 1;
        int mid;

        // 退出循环的条件是 left == right + 1，最后一次循环的时候，left == right，
        // 如果此时还没有找到目标元素，说明原数组中没有目标元素，根据题意需要在数组中
        // 插入目标元素，并返回目标元素的下标，假设目标元素target < nums[mid]，
        // 那么需要在nums[mid]左边插入target，此时target下标就是mid，而此时left == mid，
        // 直接返回left；假设目标元素target > nums[mid]，那么需要在nums[mid]右边插入target，
        // 此时target的下标就是mid + 1，而此时left == mid + 1，所以最后直接返回left
        while (left <= right) {
            mid = (left + right) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

复杂度分析：

时间复杂度： $O(\log_{2}{n})$ ，这里 $n$ 是输入数组的长度
空间复杂度： $O(1)$

3.3 在排序数组中查找元素的第一个和最后一个位置中等

原题链接：在排序数组中查找元素的第一个和最后一个位置在新窗口打开

描述：

给你一个按照非递减顺序排列的整数数组 $nums$ ，和一个目标值 $target$ 。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 $target$ ，返回 $[-1, -1]$ 。你必须设计并实现时间复杂度为 $O(log n)$ 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

$0 <= nums.length <= 10^5$
$-10^9 <= nums[i] <= 10^9$
$nums$ 是一个非递减数组
$-10^9 <= target <= 10^9$

看完这道题的题干，给我们的感觉就是，这中等类型的题目是要比简单类型要难一点，但是看到主要的关键字，我们还是很快能想到这道题应该使用二分查找算法来做。

思路1分析：

我看到这道题的第一想法，是通过二分查找找到第一个目标元素，然后从目标元素开始，分别向左右两边扩散，找到目标元素的左右边界，这个思路很简单，但是时间复杂度不再是 $O(log n)$ 了，而是介于 $O(log n)$ 和 $O(n)$ 之间，最好的时候是 $O(log n)$ ，最差就到 $O(n)$ 了，显然是不符合题意要求的。不过，这种扩散思路未来在其他的数据结构算法题中会有用武之地，所以这里我们也简单分析下：

首先我们排除掉特殊场景：数组 $nums$ 长度为 $0$ 的，目标元素 $target$ 小于数组 $nums$ 最左边值或者大于最右边值的情况，这三个场景，一定是不包含目标元素的，直接返回 $[-1, -1]$ ；
我们通过二分查找法，找到第一个目标元素，找到后，定义两个变量，分别是 $targetLeft$ 和 $targetRight$ ，并把 $mid$ 赋值给这两个变量，如果存在 $left < targetLeft$ ，那么说明当前这个目标元素离查找区间 最左边界 还有一定的距离，那么在当前目标元素左边还有可能存在目标元素，此时进行循环，循环条件就是 $left < targetLeft$ ，如果存在 $target == nums[targetLeft - 1]$ 成立，那么 $targetLeft$ 可以继续左移一位，如果某个元素不等于 $target$ 了，那么可以直接终止循环，因为再往左，也不可能找到目标元素了，因为查找区间内的元素都是非递减顺序排列的。同理，如果存在 $targetRight < right$ ，说明当前这个目标元素离查找区间 最右边界 还有一定的距离，那么在当前目标元素右边还有可能存在目标元素，此时进行循环，循环条件就是 $targetRight < right$ ，如果存在 $target == nums[targetRight + 1]$ 成立，那么 $targetRight$ 可以继续右移一位，如果某个元素不等于 $target$ 了，那么可以直接终止循环。最后直接返回 $[targetLeft, targetRight]$ 即可。
如果我们通过二分查找一个目标元素也没有找到，说明整个数组中都不包含目标元素，直接返回 $[-1, -1]$ 。

这个思路的代码实现如下所示：

代码展示：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        // 排除特殊场景：数组长度为0，或者目标元素在超出了数组的左右边界的值
        if (nums.length == 0 || target < nums[0] || target > nums[nums.length - 1]) {
            return new int[] {-1, -1};
        }

        // 定义三个变量，它们分别是左右边界的下标及中间值的下标
        int left = 0;
        int right = nums.length - 1;
        int mid;

        while (left <= right) {
            mid = (left + right) / 2;
            if (target == nums[mid]) {
                // 定义目标元素的左右边界下标为targetLeft和targetRight
                int targetLeft = mid;
                int targetRight = mid;
                while (left < targetLeft) {
                    // 目标元素和左边一位元素相同，那么目标元素的左边界下标左移一位
                    if (target == nums[targetLeft - 1]) {
                        targetLeft--;
                    } else {
                        // 提前终止循环，因为一旦元素不等于目标元素，再往左都不会再有相等的可能
                        break;
                    }
                }
                while (targetRight < right) {
                    // 目标元素和右边一位元素相同，那么目标元素的右边界下标右移一位
                    if (target == nums[targetRight + 1]) {
                        targetRight++;
                    } else {
                        // 提前终止循环，因为一旦元素不等于目标元素，再往右都不会再有相等的可能
                        break;
                    }
                }
                return new int[] {targetLeft, targetRight};
            } else if (target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        // 能走到这里，说明没有找到目标元素，直接返回[-1, -1]
        return new int[] {-1, -1};
    }
}

复杂度分析：

时间复杂度：介于 $O(\log_{2}{n})$ 和 $O(n)$ 之间，这里 $n$ 是输入数组的长度
空间复杂度： $O(1)$

思路2分析：

我们重点分析一下第二种思路：

首先我们排除掉特殊场景：数组 $nums$ 长度为 $0$ 的，目标元素 $target$ 小于数组 $nums$ 最左边值或者大于最右边值的情况，这三个场景，一定是不包含目标元素的，直接返回 $[-1, -1]$ ；
我们通过二分查找算法来寻找目标元素的最左边界和最右边界，所以我们需要两次二分查找才能完成这个任务。我们一起来想想，如何找到最左和最右边界呢？回想之前的场景：找目标元素，数组内只有一个目标元素的时候，找到直接就可以返回其下标。现在对于这种找目标元素区间的场景，我们不能直接返回已经找到的目标元素的下标，因为我们找到目标元素之后，它的左边和右边可能还有目标元素，我们需要进一步循环，去看它的左边或者右边是否还有目标元素。我们先以 示例1 来分析寻找最左边界的过程：

进入到循环体中各个变量的值：

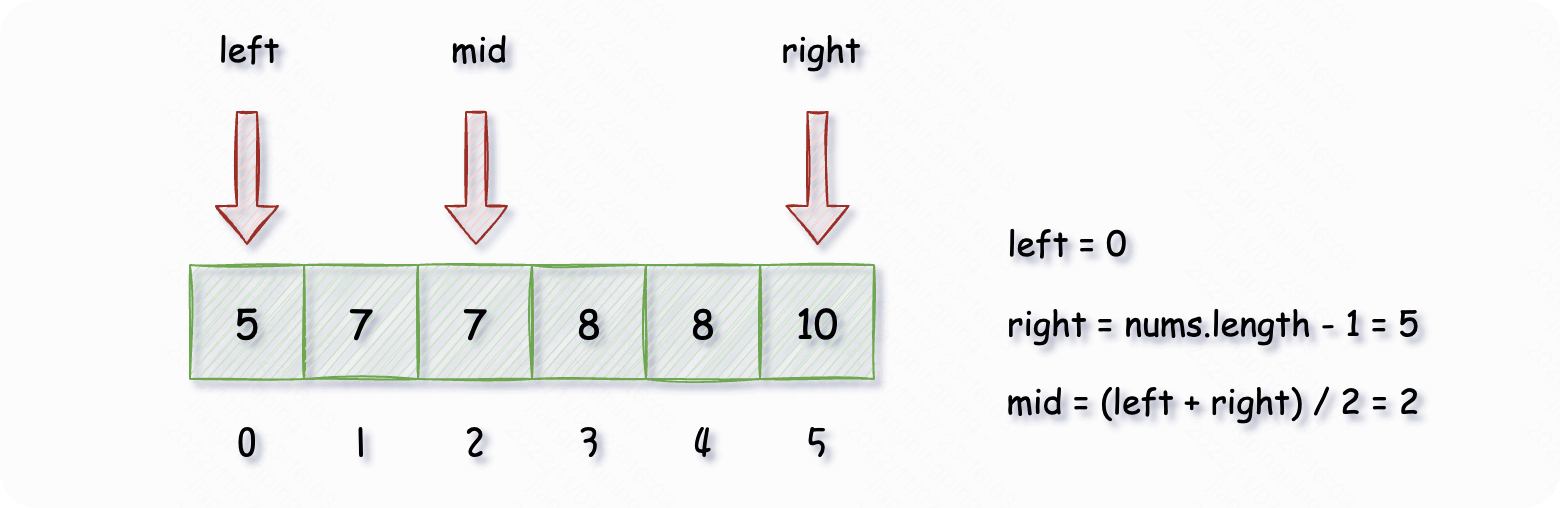
此时 $nums[mid] < target$ ，如果数组中存在目标元素，那么一定在 $mid$ 的右边，此时重新计算各个变量的值：

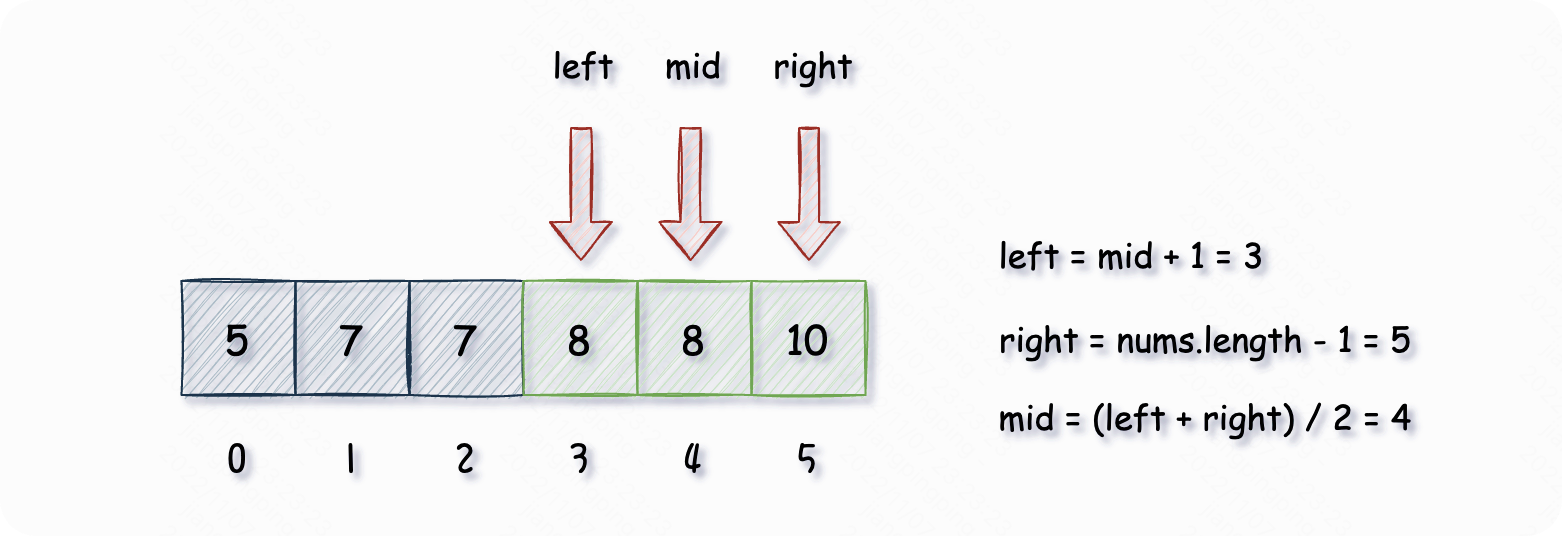
此时 $nums[mid] == target$ ，此时如果我们直接返回 $mid$ 值，肯定是不对的，我们令 $right = mid$ ，只要循环条件满足 $left < right$ ，我们可以继续循环，此时重新计算各个变量的值：

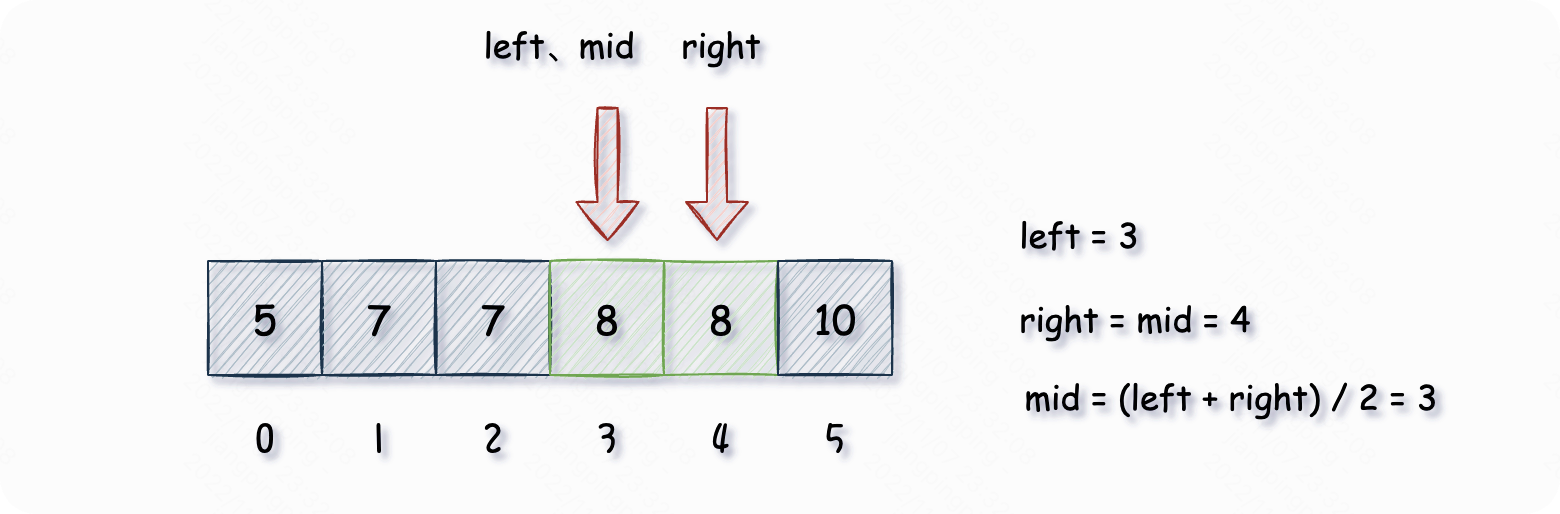
此时 $nums[mid] == target$ ，此时如果我们直接返回 $mid$ 值，可能还是不对的，我们令 $right = mid$ ，此时不在满足循环条件 $left < right$ ，退出循环前的状态是：

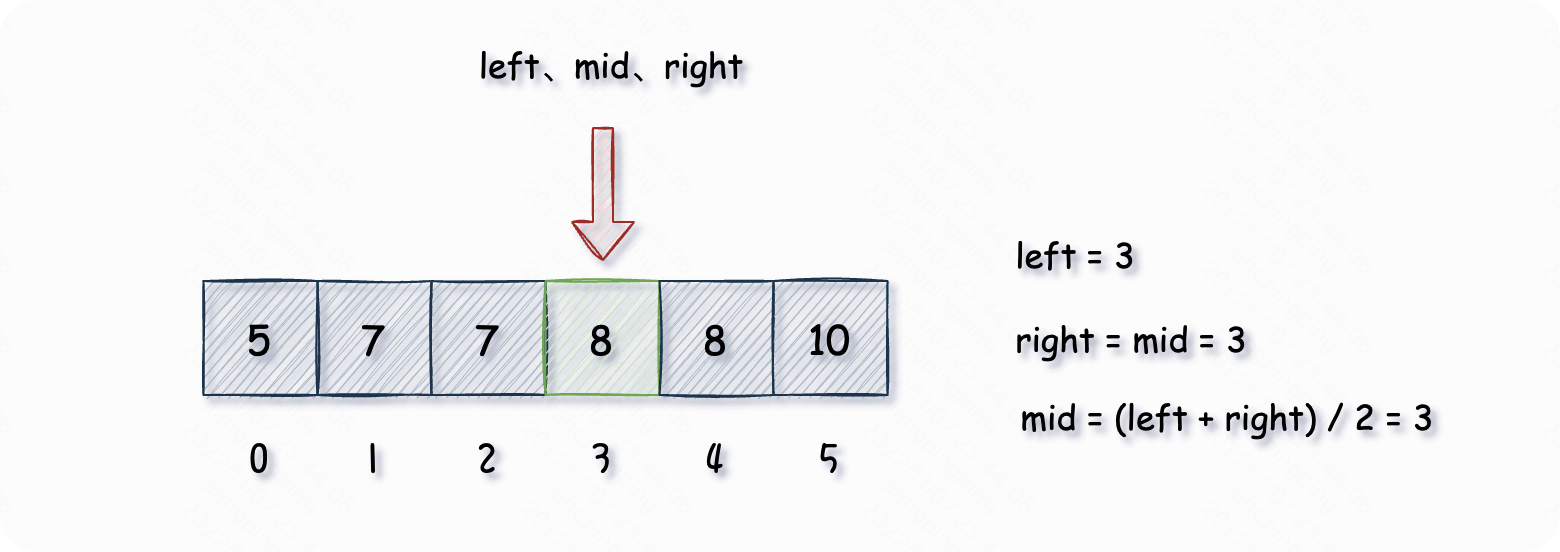
从图文中可以看出，找到左边界是靠 $right$ 不断向左靠拢，最后达到 $left == right$ 终止循环，如果满足 $nums[left] == target$ ，那么 $left$ 一定是目标元素的左边界，如果不满足，那么说明数组中没有找到目标元素，说明不存在目标元素。核心代码如下所示：

// 定义三个变量，它们分别是左右边界的下标及中间值的下标
int left = 0;
int right = nums.length - 1;
int mid;

// 寻找目标元素最左边界，是靠right不断向左靠拢，最后达到left == right终止循环
// 此时如果nums[left] == target，那么left一定是目标元素的左边界
while (left < right) {
    mid = (left + right) / 2;
    if (nums[mid] < target) {
        left = mid + 1;
    } else {
        right = mid;
    }
}

// 退出上述循环的条件是 left == right，如果此时 mums[left] != target，
// 说明整个数组中没有目标元素，直接返回[-1, -1]
if (nums[left] != target) {
    return new int[] {-1, -1};
}

找右边界的原理是一样的，需要靠 $left$ 不断向右靠拢，最后达到 $left == right$ 终止循环，如果满足 $nums[right] == target$ ，那么 $right$ 一定是目标元素的右边界，如果不满足，直接去上一个步骤中获取到的左边界作为右边界即可， 这里有一个坑需要特别注意： 找右边界过程中，计算 $mid$ 值的时候，一定要向上取整，也就是 $mid = (left + right + 1) / 2$ ，如果还是和找左边界一样，那么就会进入死循环。整体的核心代码如下所示：

代码展示：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        // 排除特殊场景：数组长度为0，或者目标元素在超出了数组的左右边界的值
        if (nums.length == 0 || target < nums[0] || target > nums[nums.length - 1]) {
            return new int[] {-1, -1};
        }

        // 定义目标元素的两个左右边界变量
        int targetLeft;
        int targetRight;

        // 定义三个变量，它们分别是左右边界的下标及中间值的下标
        int left = 0;
        int right = nums.length - 1;
        int mid;

        // 寻找目标元素最左边界，是靠right不断向左靠拢，最后达到left == right终止循环
        // 此时如果nums[left] == target，那么left一定是目标元素的左边界
        while (left < right) {
            mid = (left + right) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        // 退出上述循环的条件是 left == right，如果此时 mums[left] != target，
        // 说明整个数组中没有目标元素，直接返回[-1, -1]
        if (nums[left] != target) {
            return new int[] {-1, -1};
        }

        // 将最左边界赋值给目标元素的左边界
        targetLeft = left;

        // 重置变量
        left = 0;
        right = nums.length - 1;

        // 寻找目标元素最右边界，是靠left不断向右靠拢，最后达到left == right终止循环
        // 此时如果nums[right] == target，那么right一定是目标元素的右边界
        while (left < right) {
            mid = (left + right + 1) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid;
            }
        }

        // 这里需要判断下nums[right] == target ？如果不是，那么说明数组中只有一个目标元素，此时左右边界都是同一个数
        targetRight = nums[right] == target ? right : targetLeft;

        return new int[] {targetLeft, targetRight};
    }
}

复杂度分析：

时间复杂度： $O(\log_{2}{n})$ ，这里 $n$ 是输入数组的长度
空间复杂度： $O(1)$

3.4 x 的平方根简单

原题链接：x 的平方根在新窗口打开

描述：

给你一个非负整数 x，计算并返回 x 的算术平方根 。由于返回类型是整数，结果只保留整数部分 ，小数部分将被舍去。

注意： 不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例1：

输入：x = 4
输出：2

示例2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

$0 <= x <= 2^{31} - 1$

思路分析：

根据题意，我们很容易找到这样的隐含条件，其实就是求 $k$ 值，而这个 $k$ 值满足条件 $k^2 <= x$ ，且 $k$ 在 $0$ 到 $x$ 之间。转换思路就是在递增数组 $[0, 1, ..., k, ..., x]$ 中找到目标值 $k$ ，目标值 $k$ 满足条件 $k^2 <= x$ ，思路转换后，我们很快就可以发现，可以使用二分查找法来解决这个问题。

代码展示：

class Solution {
    public int mySqrt(int x) {
        // 定义三个变量，它们分别是左右边界及中间值的下标，由于x有可能为0，所以设置右边界下标为x
        // 这样组成的数组可以理解为[0, 1, 2, ..., x]
        int left = 0;
        int right = x;
        int mid;

        // 定一个变量ans，用来记录x的平方根整数部分值，它存在这样的关系：ans^2 <= x
        int ans = 0;

        while (left <= right) {
            // 这么计算mid，是防止整型溢出，因为x的取值范围是：0 <= x <= 2^31 - 1
            mid = left + (right - left) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return ans;
    }
}

复杂度分析：

时间复杂度： $O(\log_{2}{n})$ ，这里 $n$ 是输入数组的长度
空间复杂度： $O(1)$

3.5 寻找重复数中等

原题链接：寻找重复数在新窗口打开

描述：

给定一个包含 $n + 1$ 个整数的数组 $nums$ ，其数字都在 $[1, n]$ 范围内（包括 $1$ 和 $n$ ），可知至少存在一个重复的整数。假设 $nums$ 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 $nums$ 且只用常量级 $O(1)$ 的额外空间。

示例1：

输入：nums = [1,3,4,2,2]
输出：2

示例2：

输入：nums = [3,1,3,4,2]
输出：3

提示：

$1 <= n <= 105$
$nums.length == n + 1$
$1 <= nums[i] <= n$
$nums$ 中 只有一个整数 出现 两次或多次 ，其余整数均只出现一次

思路分析：

根据题意可知，数组 $nums$ 中有 $n + 1$ 个整数，且这些数字都在 $[1, n]$ 范围内，那么由此可知，至少 存在一个重复的整数 ，这里基本可以分为两种情况，我们假设有重复的数字是 $target$ ：

第一种是， 仅存在一个重复的整数，也就是 $target$ 出现了两次 ，数组 $nums$ 中， $1$ 到 $n$ 中每个数都占了一个，且仅存在一个重复的数，一共是 $n + 1$ 个数字。
第二种是， 整数 $target$ 重复出现三次（或三次以上） ，这种情况，在数组 $nums$ 中， $1$ 到 $n$ 中必然有 某个数字（或某几个） 没有出现在数组中，被 $target$ 给代替了。

第一种情况很好理解，第二种情况中，当整数 $target$ 重复出现三次或三次以上，那么到底有几个数字被 $target$ 替代呢？其实也很好理清楚：

当 $target$ 出现两次，那么 $[1, n]$ 中没有数字被 $target$ 替代了，它对应第一种情况；
当 $target$ 出现三次，那么 $[1, n]$ 中必然有一个数字被 $target$ 替代了；
当 $target$ 出现四次，那么 $[1, n]$ 中必然有两个数字被 $target$ 替代了，然后以此类推。

分析后就可以得出基本结论，想知道几个数字被 $target$ 代替了，其实就是 $target$ 出现的次数减 $2$ 的关系，这样就可以很快知道 $[1, n]$ 范围内有几个数字没有出现。

# 第2节 数组的二分查找算法

# 一、经典案例

# 二、二分查找算法

# 2.1 什么是二分查找

# 2.2 使用语言实现二分查找算法

# 2.3 二分查找中的细节分析

# 2.3.1 搜索区间的开闭问题

# 2.3.2 中间值下标取值问题

# 2.3.3 判断条件设置问题

# 2.3.4 搜索区间选择问题

# 2.4 排除法思路介绍

# 三、精选练习题

# 3.1 猜数字大小 简单

# 3.2 搜索插入位置 简单

# 3.3 在排序数组中查找元素的第一个和最后一个位置 中等

# 3.4 x 的平方根 简单

# 3.5 寻找重复数 中等

# 3.6 Pow(x, n) 中等

第2节数组的二分查找算法

一、经典案例

二、二分查找算法

2.1 什么是二分查找

2.2 使用语言实现二分查找算法

2.3 二分查找中的细节分析

2.3.1 搜索区间的开闭问题

2.3.2 中间值下标取值问题

2.3.3 判断条件设置问题

2.3.4 搜索区间选择问题

2.4 排除法思路介绍

三、精选练习题

3.1 猜数字大小简单

3.2 搜索插入位置简单

3.3 在排序数组中查找元素的第一个和最后一个位置中等

3.4 x 的平方根简单

3.5 寻找重复数中等

3.6 Pow(x, n) 中等